L0正则:
我们要讨论的第一个规范是L0规范。根据定义,x的L0范数是
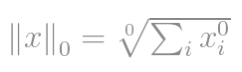
严格来说,L0范数实际上不是一个范数。它是基数函数,其定义形式为L0-norm,尽管许多人称其为范数。使用它有点棘手,因为其中存在零次幂和零次方。显然,任何x> 0都将变为1,但是零次幂(尤其是零次幂)的定义问题使这里变得混乱。因此,实际上,大多数数学家和工程师都使用L0-范数的此定义:
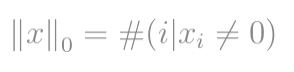
那就是向量中非零元素的总数。
例如,向量(0,0)和(0,2)的L0范数为1,因为只有一个非零元素。
L0范数的一个很好的实用示例是当具有两个向量(用户名和密码)时给出Nishant Shukla的示例。 如果向量的L0范数等于0,则登录成功。 否则,如果L0范数为1,则意味着用户名或密码不正确,但都不正确。 最后,如果L0规范为2,则意味着用户名和密码都不正确。
L1正则:
L1范数是空间中向量的大小之和。 这是测量向量之间距离的最自然的方法,即向量分量的绝对差之和。 在此规范中,向量的所有分量均被加权。
根据范数的定义,x的L1-范数定义为
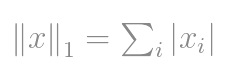
如果为两个向量或矩阵之间的差计算L1范数,则即
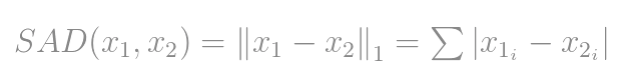
在计算机视觉科学家中,它被称为绝对差总和(SAD)。
在信号差测量的更一般情况下,可以通过以下方法将其缩放为单位向量:
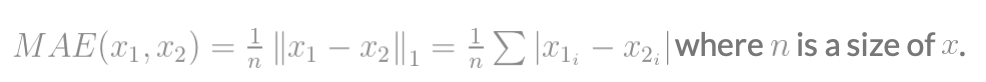
例如,向量X = [3,4],L1范数的计算公式为:

L2正则:
是最流行的规范,也称为欧几里得规范。 这是从一个点到另一个点的最短距离。同样的例子,L2 的算法如下:
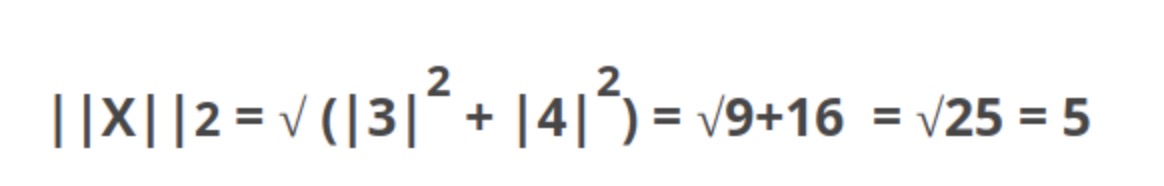
另外我们可以将L1范数实现正则化的线性回归模型称为lasso回归,将L2范数实现(平方)以正则化的线性回归模型称为岭回归。
L1和L2正则化都可以通过对系数进行缩小(施加惩罚)来防止过度拟合。 L2(Ridge)将所有系数按相同的比例缩小,但没有消除,而L1(Lasso)可以将某些系数缩小到零,执行变量选择。
Lasso
lasso回归是一种使用收缩的线性回归。收缩是数据值向中心点(如均值)收缩的地方。lasso是稀疏的模型(即参数较少的模型)。这种特殊类型的回归非常适合显示高水平线性线性关系的模型。
首字母缩写词“ LASSO”代表最小绝对收缩和选择算符。
回想lasso最小化问题可以表示为:
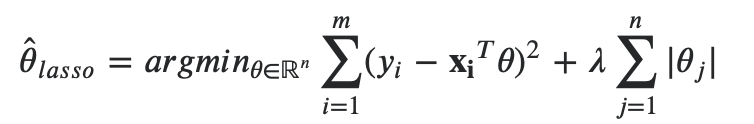
可以看成是两个项的最小值:𝑂𝐿𝑆+𝐿1
第一个OLS项可以表示为(𝑦−𝑋𝜃)𝑇(𝑦−𝑋𝜃),这会产生一个以最大似然估计器为中心的椭圆等高线图。
第二个𝐿1项是以0为中心的菱形方程(或较大尺寸的菱形)
约束优化的解位于两个函数的轮廓之间的交点,并且该交点随of的函数而变化。对于𝜆 = 0,解为MLE,对于𝜆 =∞,解为[ 0,0]
由于在菱形的顶点处,一个或多个变量的值为0,因此一个或多个系数的值恰好等于0的可能性不为零。
如下图所示:

岭回归
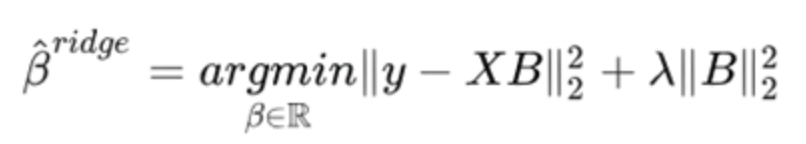
岭回归通过使用L2范数减少了系数的大小,从而减少了模型中的高复杂度。 它极大地帮助我们过度拟合和处理离群值。 同样考虑到L2范数的性质,它是稳定的,并给出了唯一的全局最小值。
这是减少过度拟合的正则化方法。
我们尝试使用一条过度拟合训练数据的趋势线,因此,其方差比OLS高得多。 岭回归的主要思想是要增加一条不适合训练数据的新线。 换句话说,我们将一定的“偏差bias”引入趋势线。

我们在实践中要做的是引入一个称为Lambda的偏差bias,惩罚函数为:lambda * slope ^ 2。
Lambda是惩罚项,此值称为Ridge回归或L2。
L2分是二次的:lambda slope ^ 2:没有一个系数(斜率)非常大。
当Lambda = 0时,惩罚也为0,因此我们只是在最小化残差平方和。
当Lambda渐近增加时,我们到达接近0的斜率:因此,LAMBDA越大,我们的预测对自变量的敏感性就越小。
Lambda是控制偏差方差的调整参数,我们通过交叉验证来估计其最佳值。
如果L1和L2对比,L2比L1要好一些,因为L2之后,精度更好且较好适应、拟合。L1的效果在处理稀疏数据时候比较棒,且有利于稀疏数据的特征。