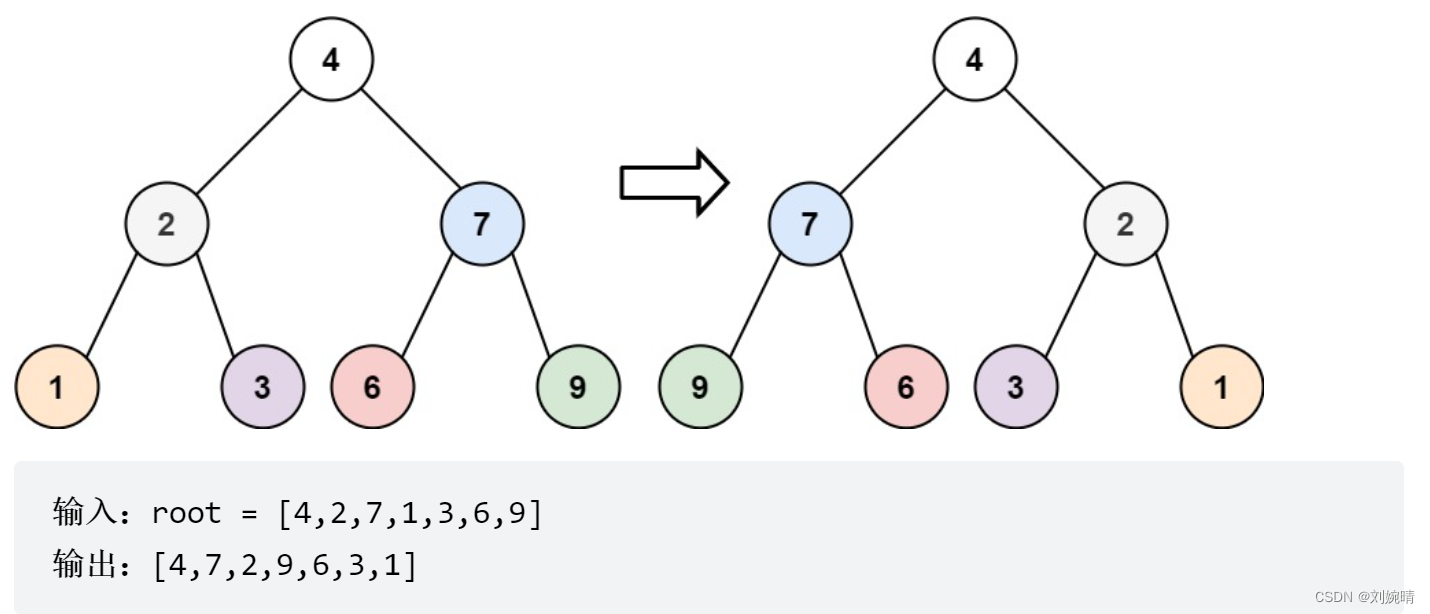
题目

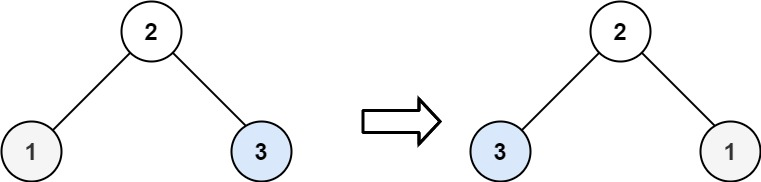
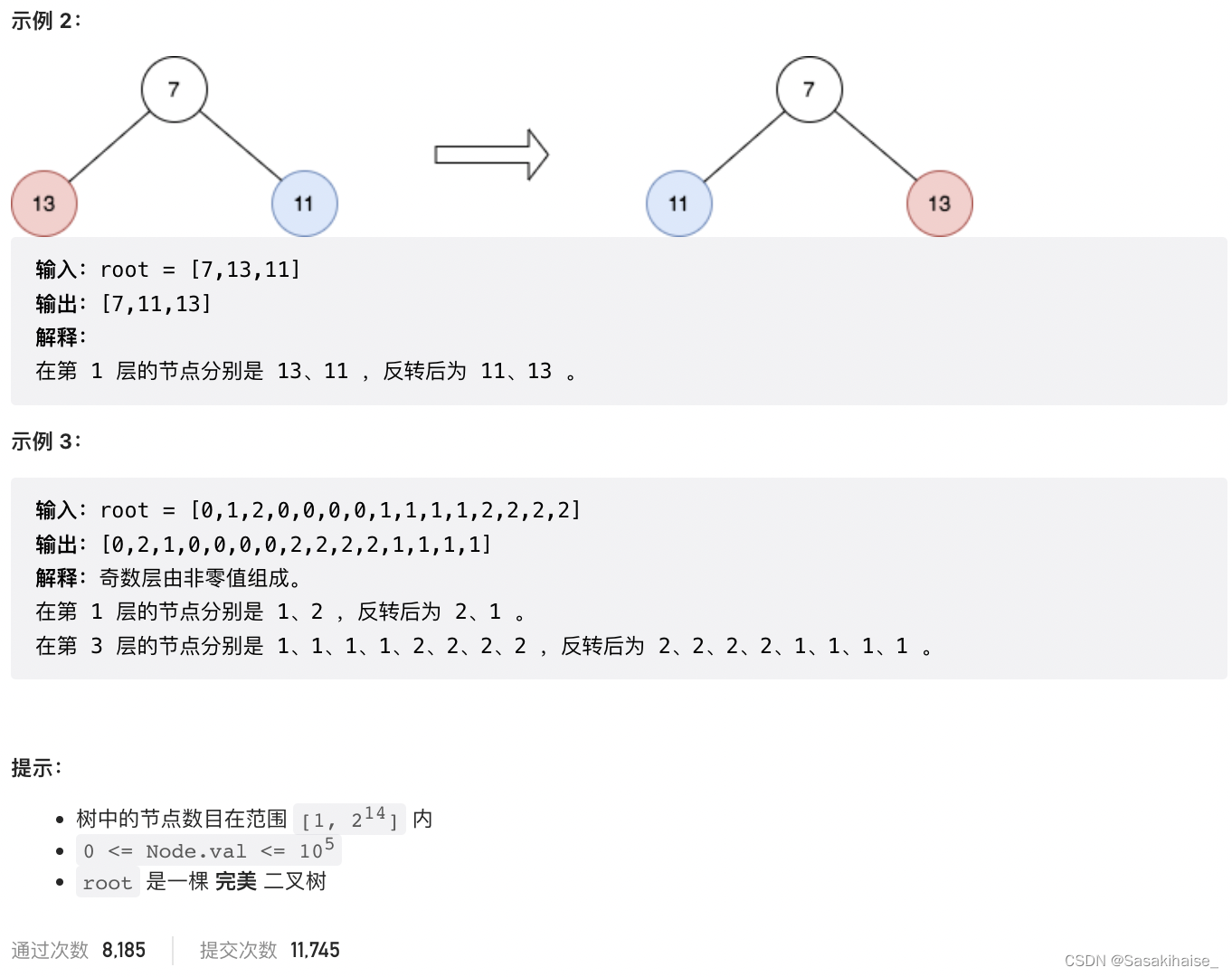
给你一颗二叉树的根节点root，请你翻转该二叉树，并且返回其根节点。
在这里插入图片描述

思路①

如何判定二叉树是否翻转？

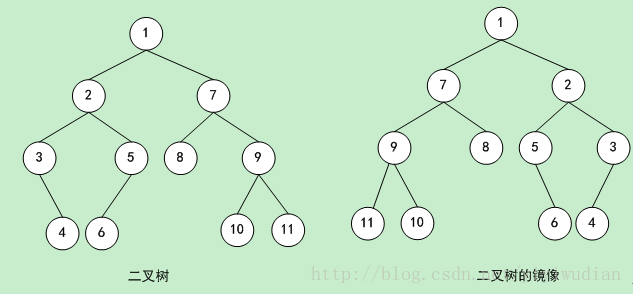
左右子树需要交换，左右子树内部的左右子节点也需要交换位置。
根节点root表示：
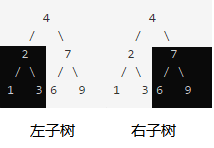
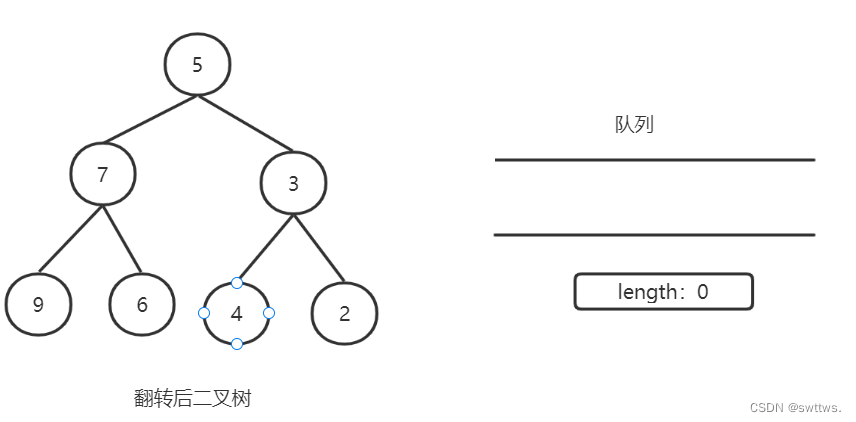
首先交换左右子树，递归压栈压到底部，然后开始交换，位于底部的、左右子树都是null的子树，首先被翻转。随着递归向上返回，子树都被一个个翻转，整颗二叉树也随即翻转到位。

思路①代码

const invertTree = (root) => {if (root == null) { // 遍历到null节点时，不用翻转，直接返回它本身return root;}invertTree(root.left);invertTree(root.right);const temp = root.left;root.left = root.right;root.right = temp;return root;
};

思路②

首先考虑先交换左右子树，内部子树还没有翻转——这部分交给递归处理。
其次在交换这一步的操作，放在递归之前。
题目的要求是在递归压栈之前完成。

思路②代码

const invertTree = (root) => {if (root == null) { // 遍历到null节点时，不用翻转，直接返回它本身return root;}const temp = root.left;root.left = root.right;root.right = temp;// 内部的翻转交给递归去做invertTree(root.left);invertTree(root.right);return root;
};

总结

两种分别是前序遍历和后序遍历，并且基于DFS深度优先遍历，如下实例所示：

整数排列：给定数字N，给出按照字典序的排列。

代码，C++实现：

//排列数字，给定整数N，按照字典序排列
#include <iostream>
using namespace std;const int N = 10;int n;
int path[N];  //用一个全局数组实现存储方法状态
bool st[N];   //判定一个数是否用过？void dfs(int u) {if (u == n) {//说明一个排列已经把所有位置排满了，当前位置输出就行for (int i = 0; i < n; i++) {printf("%d ", path[i]);}puts("");return;}/*u < n,说明还没有填完,也就是还没有得到一种方案数枚举一下当前这个位置可以填哪些数 */for (int i = 1; i <= n; i++) {if (!st[i]) {//找到了一个没有被用过的数path[u] = i;//记录该数已经被使用过st[i] = true;//状态处理好之后递归到下一层dfs(u + 1);//恢复现场，path[u] = 0没有必要，因为会被不断的覆盖st[i] = false;}}
}int main() {cin >> n;dfs(0);return 0;
}

实例2，八皇后问题，给出代码如下：

时间复杂度，O(n*n!)，较优解法，实例为4 × 4棋盘，4个皇后。

//八皇后问题
#include <bits/stdc++.h>
using namespace std;
const int N = 20;int n;
char g[N][N]; 				//表示方案数
bool col[N], dg[N], udg[N]; //分别检验同一列、正反对角线是否只有一个皇后void dfs(int u) {if (u == n) {//当找到一组方案的时候，输出for (int i = 0; i < n; i++) {puts(g[i]);}puts("");return ;}//从前往后枚举u行，看皇后应该在哪一列for (int i = 0; i < n; i++) {if (!col[i] && !dg[u + i] && !udg[n - u + i]) {//某一列，某条对角线都没有元素放入过g[u][i] = 'Q';//已经有皇后元素col[i] = dg[u + i] = udg[n - u + i] = true;dfs(u + 1);//恢复现场col[i] = dg[u + i] = udg[n - u + i] = false;g[u][i] = '*';//到这可以发现if语句完全对称}}
}int main() {cout << "请输入整数：" << endl;cin >> n;for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {g[i][j] = '*';}}dfs(0);return 0;
}