1.串的定义与基本操作

1.1定义

1.2基本操作

2.串的存储结构

2.1顺序存储

2.2链式存储

3.字符串的模式匹配算法（“查找”章节）

3.1朴素模式匹配算法

3.2KMP算法

3.2.1算法思想

3.2.2算法代码实现

3.2.3求next数组和nextval数组（掌握手算）

1.串的定义与基本操作

1.1定义

数据结构三要素：逻辑结构（定义）、数据运算（基本操作）、存储结构（物理结构）

串，即字符串(String），是由零个或多个字符组成的有限序列。一般记为 $s="a_{1},a_{2},...,a_{n} "$
其中，s是串名，引号（单/双引号都可）括起来的字符序列是串的值； $a_{i}$ 可以是字母、数字或其他字符；字符下标从1开始，串中字符的个数n称为串的长度。n=0时的串称为空串（用∅表示）。

子串：串中任意个连续的字符组成的子序列。主串:包含子串的串。
字符在主串中的位置：字符在串中的序号。（注意位序从1开始，而不是0）
子串在主串中的位置：子串的第一个字符在主串中的位置。

空串VS空格串：空串——n=0；空格串——串的值是若干空格字符（空格：00100000）

1B/char

串VS线性表：

串是一种特殊的线性表，数据元素之间呈线性关系。

区别：串的数据对象限定为字符集（如中文字符、英文字符、数字字符、标点字符等)；串的基本操作，如增删改查等通常以子串为操作对象。

1.2基本操作

假设有空串T=""，主串S="iPhone 11 Pro Max?”，字串W=“Pro"

StrASSign(&T,charS)//赋值操作。把串T赋值为chars。
StrCopy(&T,S)//复制操作。由串S复制得到串T。
StrEmpty(S)//判空操作。若S为空串，则返回TRUE，否则返回FALSE。
StrLength(S)//求串长。返回串S的元素个数。
ClearString(&S)//清空操作。将S清为空串。
DestroyString(&S)//销毁串。将串S销毁（回收存储空间）。
Concat(&T,S1,S2)//串联接。用T返回由S1和S2联接而成的新串
SubString(&Sub,S,pos,len)//求子串。用Sub返回串S的第pos个字符起长度为len的子串。
Index(S,Sub)//定位操作。若主串S中存在与串Sub值相同的子串，则返回它在主串S中第一次出现的位置;否则函数值为0。
StrCompare(S,T)//比较操作。若S>T，则返回值>O;若S=T，则返回值=0;若S<T，则返回值<O。

Concat要考虑存储空间的问题；StrCompare比较的是字符在计算机中存储的二进制数的大小。

字符集编码

a：01100001；c：01100011；空格：00100000

任何数据存到计算机中一定是二进制数。需要确定一个字符和二进制数的对应规则这就是“编码”

y = f(x)
字符集——函数定义域；编码——函数映射规则f；y——对应的二进制数

“字符集”:
英文字符——ASCII字符集；中英文——Unicode字符集（基于同一个字符集x，可以有多种编码方案f,如:UTF-8，UTF-16）
注:采用不同的编码方式，每个字符所占空间不同，考研中只需默认每个字符占1B即可（256个字符）。

乱码问题：解码错误导致的

基本操作的实现：

//一些简单操作的实现方法
StrEmpty(S)//S.length==0？
StrLength(S)//return S.length
ClearString(&S)//S.length=0(逻辑上的清空，字符还在存储空间里）//求子串。用Sub返回串S的第pos个字符起长度为len的子串。
bool SubString(SString &Sub,SString S,int pos,int len){if(pos+len > S.length) return false; //字串范围越界for(int i=pos;i<pos+len;i++){Sub[i-pos+1] = ch[i];} Sub.length = len;return true;
}
//比较操作。若S>T，则返回值>O;若S=T，则返回值=0;若S<T，则返回值<O。
int StrCompare(SString S,SString T){for(int i=1;i<S.length && I<T.length ;i++){if(S.ch[i] != T.ch[i]) return  S.ch[i] - T.ch[I];}//扫描过的字符都相同，则串长度大的串更大 return S.length - T.length;
}
//定位操作。若主串S中存在与串Sub值相同的子串，则返回它在主串S中第一次出现的位置;否则函数值为0。
int Index(SString S,SString Sub){ //结合上面两个操作 int i, Slen=StrLength(S), Sublen=StrLength(Sub); //主串S与所给子串Sub的长度 SString temp;                       //用于暂存从主串里取到的子串while(i<=Slen-Sublen+1){             //遍历到主串中最后一个同长子串的位置 SubString(temp,S,1,Sublen);if(StrCompare(temp,Sub)!=0) ++i;//从主串里取到的子串与所给Sub不同，则从主串里取下一个子串 else return i;                  //若相同则找到了所给Sub在主串中出现的位置i } return 0;                           //从主串里取到的所有子串与所给Sub都不同，则S中不存在所给Sub 
}

Index（S,Sub）中取子串的次数（对比次数） i <=Slen-Sublen+1

注意：主串S中长度为Sublen的子串的个数为Slen-Sublen+1 ；Index（S,Sub）与朴素模式匹配算法思路一致

2.串的存储结构

存储结构不同，运算的实现方式不同。

2.1顺序存储

//静态数组（定长顺序存储） 
#define MAXLEN 255
typedef struct{char ch[MAXLEN]; //每个分量存储一个字符 int length;      //串的实际长度 
}SString;            //函数结束，系统自动回收 //动态数组（堆分配存储 ）
typedef struct{char *ch;        //ch指向串的基地址 int length;      //串的长度 
}HString; 
HString S;
S.ch = (char *)malloc(MAXLEN*sizeof(char)); //malloc申请的空间在堆区（heap）,手动free释放存储空间 
S.length = 0;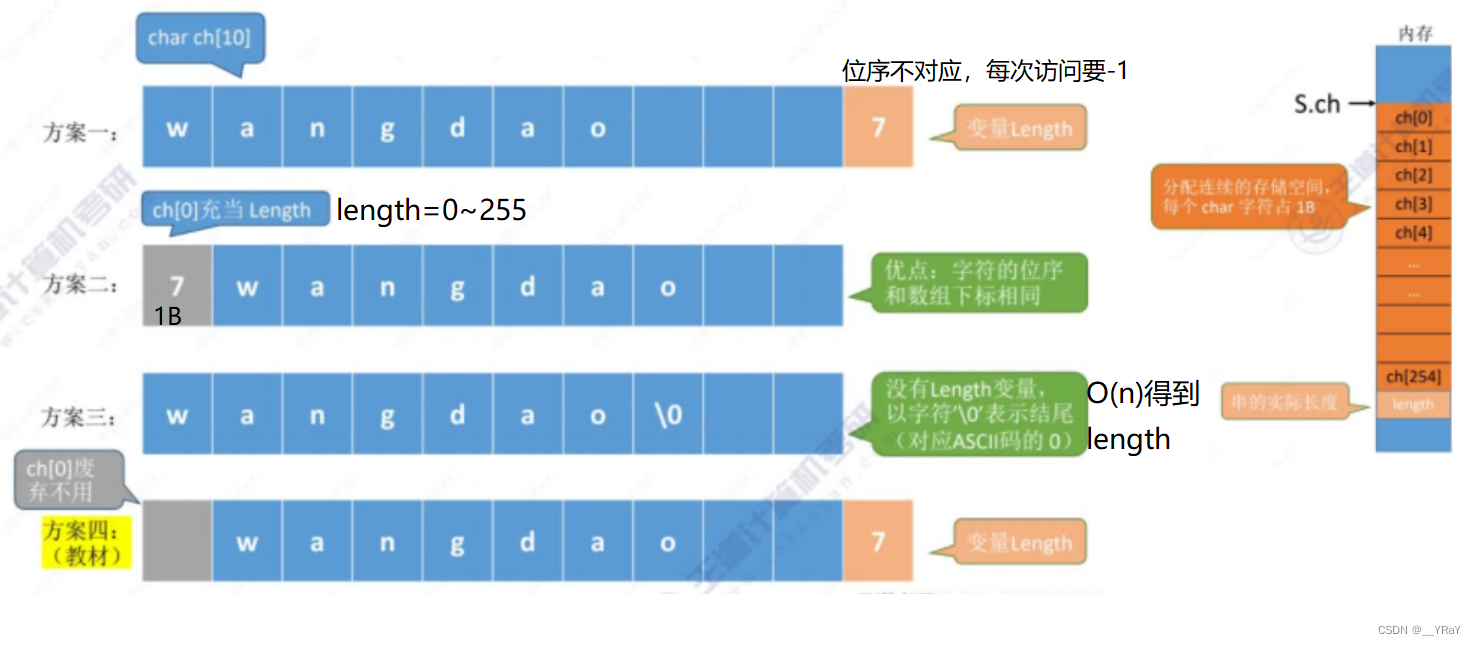

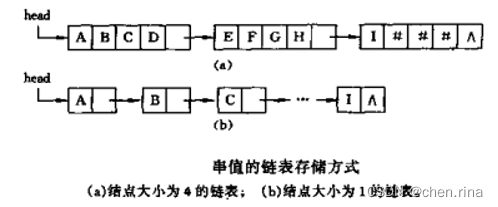
2.2链式存储

typedef struct StringNode{char ch;        //每个节点存1个字符 1Bstruct StringNode *next;          //4B
}StringNode , *String;                //存储密度低（字符1B+指针4B),可以让每个节点多存些字符
//推荐下面的定义： 
typedef struct StringNode{char ch[4];     //每个节点存4个字符 4Bstruct StringNode *next;          //4B
}StringNode , *String;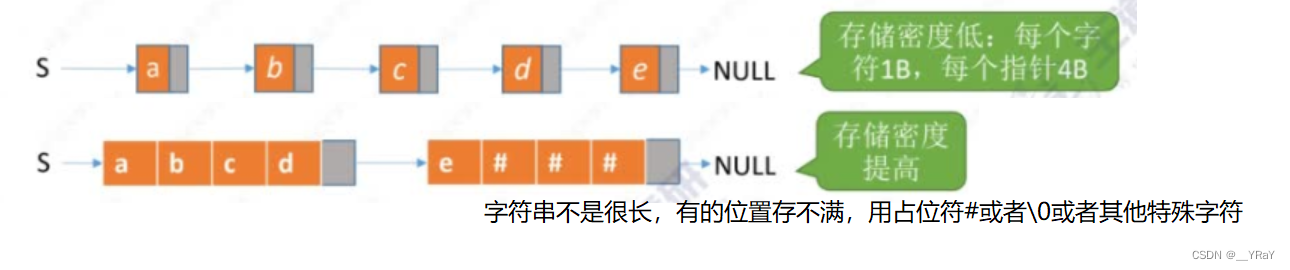

顺序串和链式串的优缺点结合顺序表和链式表分析

3.字符串的模式匹配算法（“查找”章节）

Index(SString S,SString Sub)在不结合SubString和StrCompare两个操作时如何实现？

模式匹配——search功能；在主串中找到与模式串相同的子串，并返回其所在位置。

主串；模式串（所要找到的子串）

子串――主串的一部分,一定存在；模式串――不一定能在主串中找到

模式匹配的两种算法：朴素模式匹配算法；KMP算法

3.1朴素模式匹配算法

思路：（暴力穷举所有子串进行匹配）与前面介绍的Index（S,Sub）思路一致

主串长度为n，模式串长度为m；

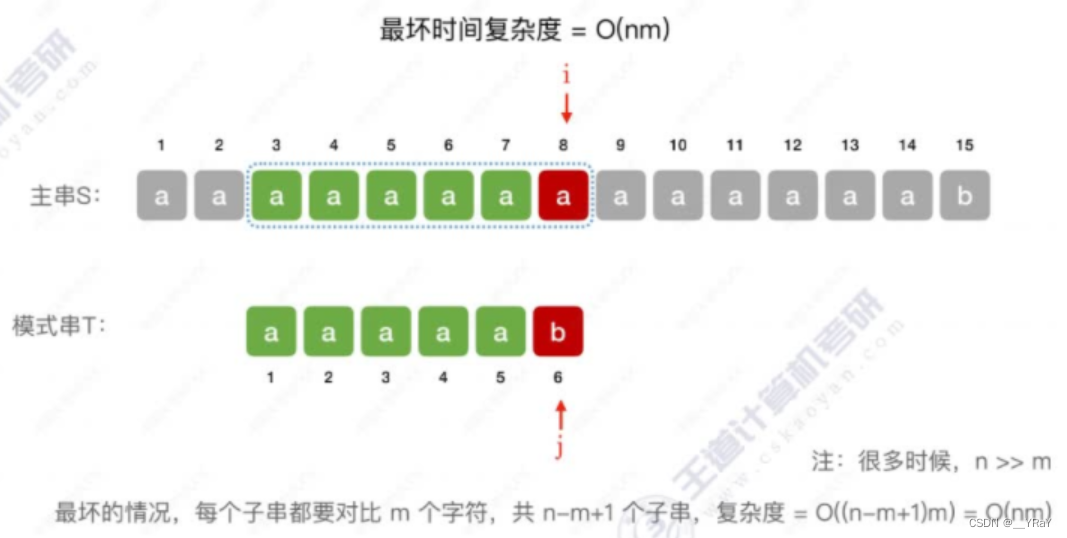
朴素模式匹配算法∶将主串中所有长度为m的子串依次与模式串对比（最多对比 n-m+1个子串），直到找到一个完全匹配的子串或所有的子串都不匹配为止。

指针回退的关键：i = i-j+2; j=1;

//S:主串；T:模式串 
int Index(SString S,SString T){int i=1,j=1;while(i<=S.length && j<=T.length){//对比 S.length-T.length+1次 if(S.ch[i] == T.ch[j]){++i;++j;//当前字符匹配，对比后继字符 }else{//匹配到不相等的字符时，指针回退，重新匹配 i = i-j+2;j = 1; }}if(j>T.length)	return i-T.length;//模式串的字符与子串全部匹配else return 0; 
}

最坏（最后一个子串与模式串匹配）时间复杂度：O(nm) 其中m=模式串长； n=主串长

3.2KMP算法

3.2.1算法思想

由D.E.Knuth，J.H.Morris和V.R.Pratt提出，因此称为KMP算法。基于朴素模式匹配算法思想优化而来。

朴素模式匹配算法：需要对比n-m+1个子串；KMP算法：根据对每次匹配时，当前字符之前的字符是已知的，根据这一点，可以跳过一些对比，对朴素模式匹配算法进行优化。

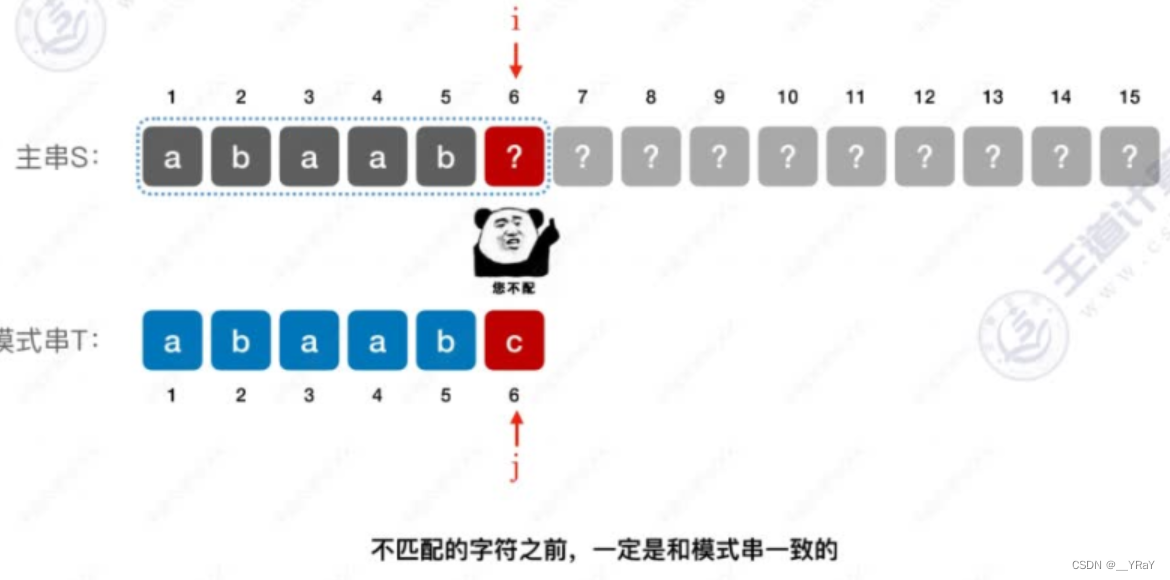
下一次匹配时 i 和 j 要调到什么位置，是该算法要思考的问题。

i 跳到何位置？——next数组/nextval数组（掌握手算next数组/nextval数组⭐）

j 跳到何位置？——主串指针不需要回溯（好马不吃回头草）

3.2.2算法代码实现

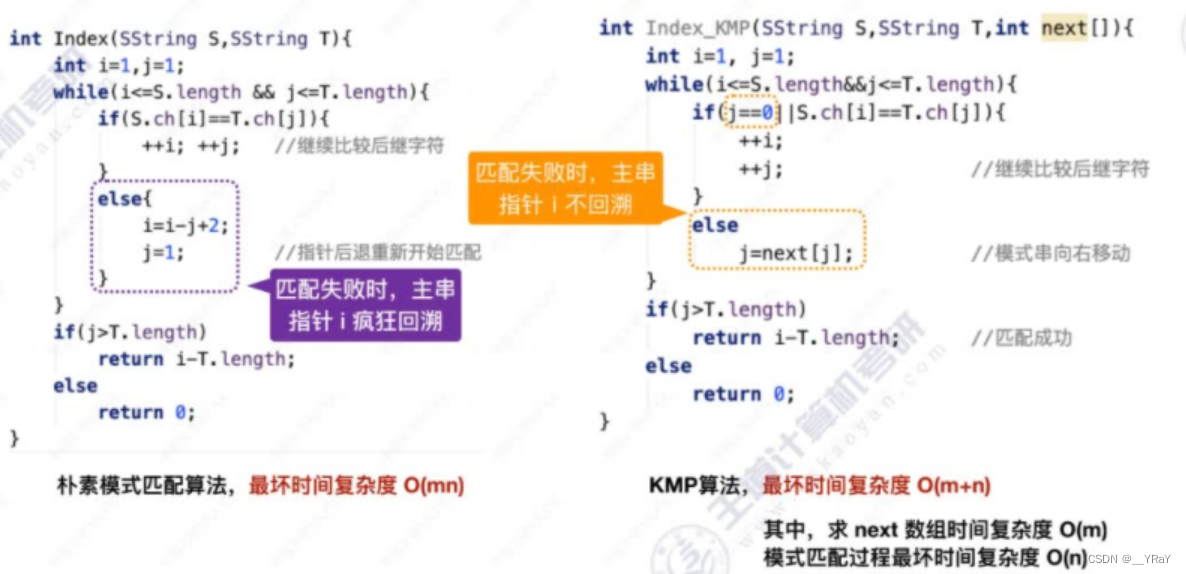
int Index_KMP(SString S,SString T,int next[]){int i=1,j=1;while(i<=S.length && j<=T.length){if(S.ch[i]==T.ch[i] || j==0){++i;++j;//比较后续字符 }else{j = next[j];//模式串的第j个位置不匹配，模式串指针j要根据next数组回溯 }}if(j>T.length) return i-T.length; //匹配成功else return 0; 
}

算法复杂度：O(m+n) = 求next数组复杂度O(m) + 最坏匹配复杂度O(n）

朴素模式匹配算法 VS KMP算法：

3.2.3求next数组和nextval数组（掌握手算）

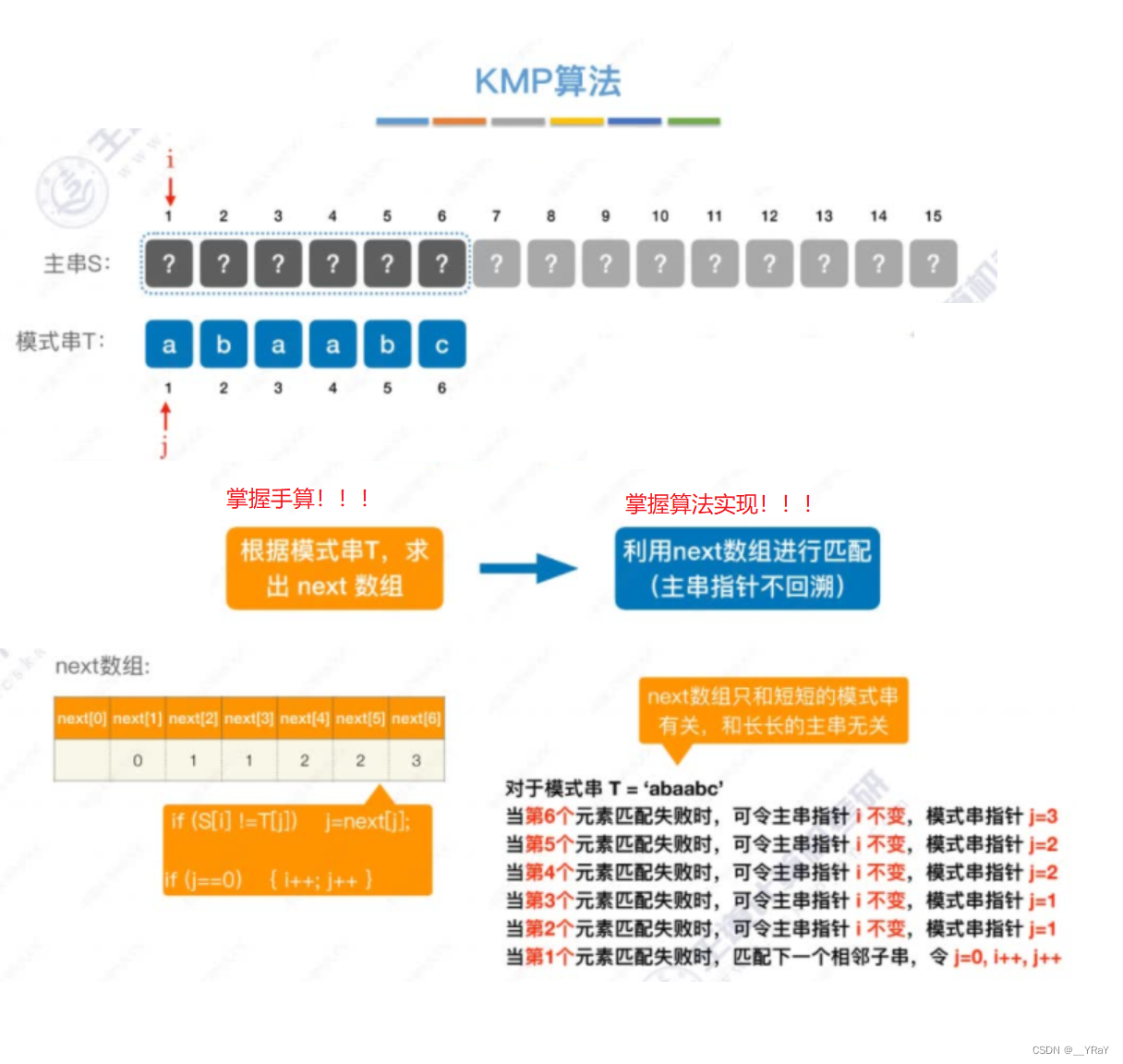
next数组的作用：当模式串的第 j 个字符失配时，从模式串的第 next[j] 的继续往后匹配

求法：

next[1]都无脑写0；

next[2]都无脑写1；
其他next：在不匹配的位置前，划一根美丽的分界线，模式串一步一步往后退，直到分界线之前“能对上”，或模式串完全跨过分界线为止。此时j指向哪儿，next数组值就是多少

任何模式串都一样，第一个字符不匹配时，只能匹配下一个子串，因此，往后余生，next[1]都无脑写0；

任何模式串都一样，第2个字符不匹配时，应尝试匹配模式串的第1个字符,因此，往后余生，next[2]都无脑写1；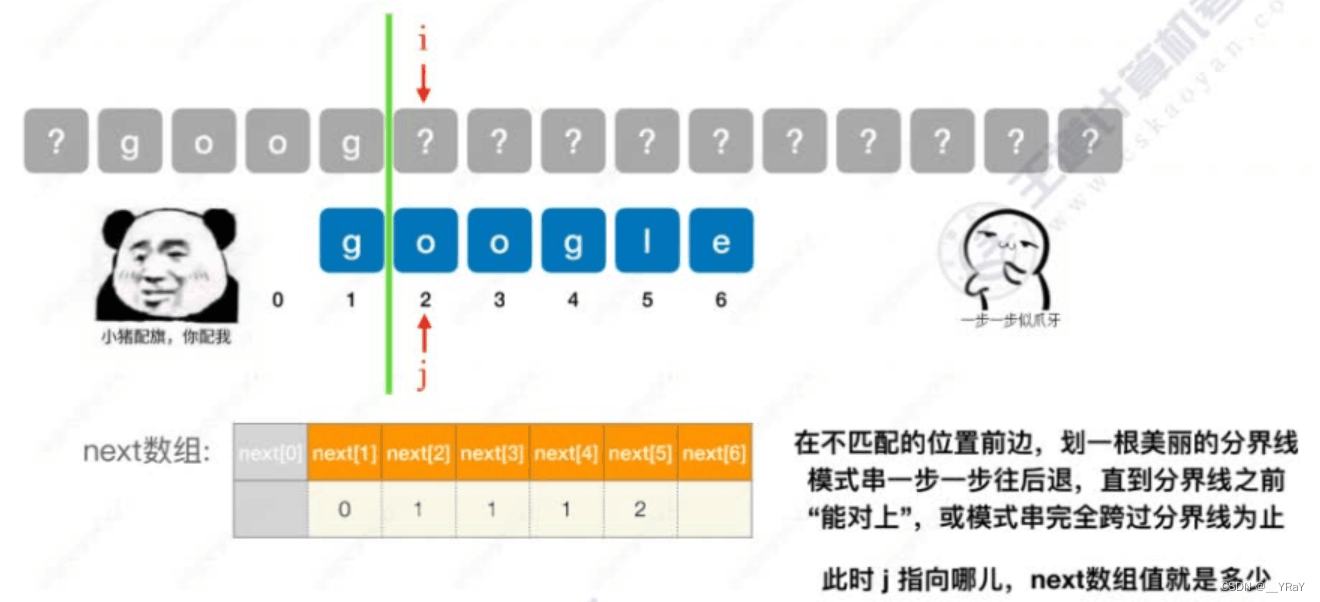

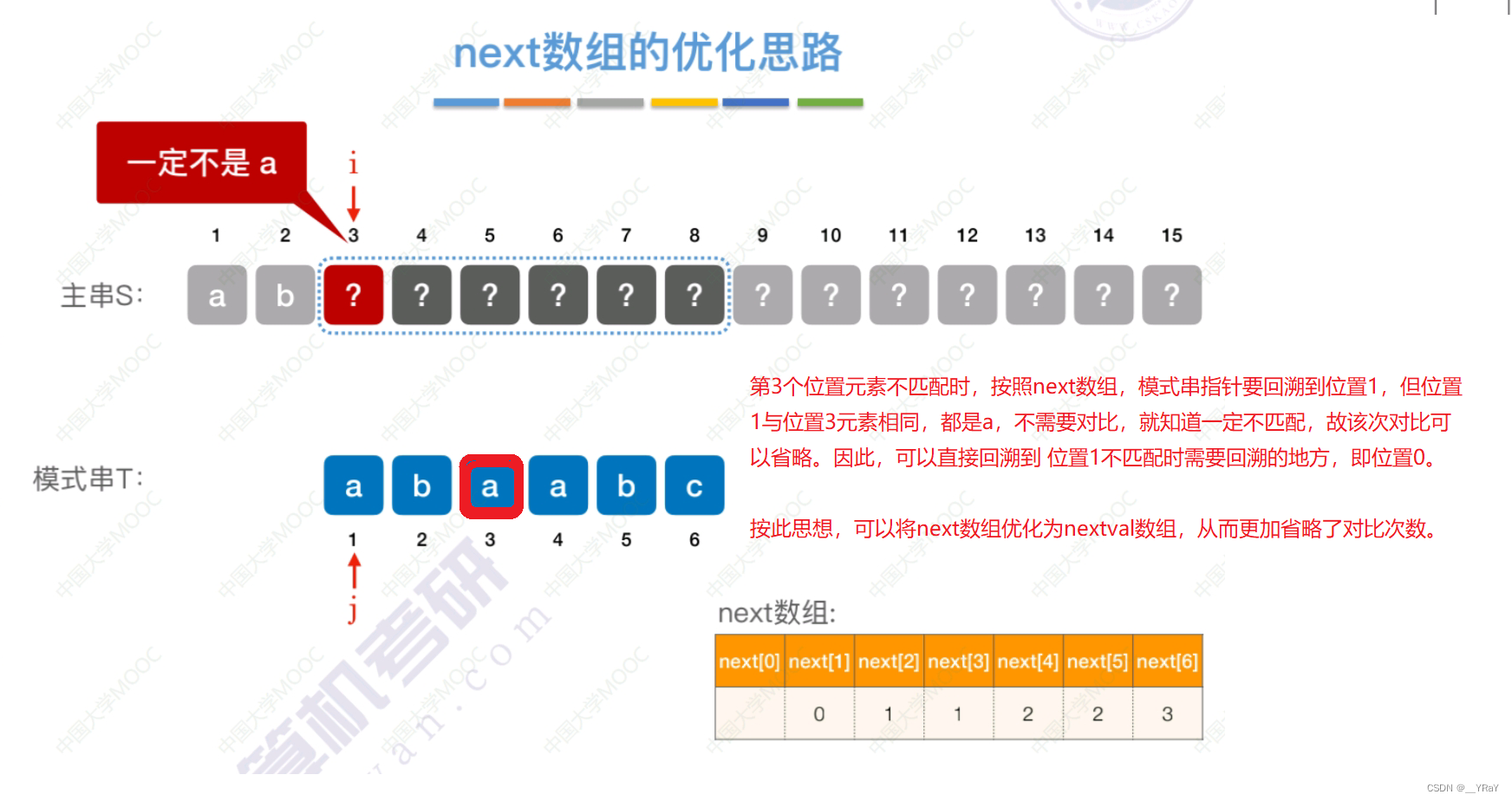
求next数组过程中，还有未利用的信息，就是可以确定当前失配的元素一定不是要匹配的元素，依此又可以省略一些对比——

分析：

第3个位置元素不匹配时，按照next数组，模式串指针要回溯到位置1，但位置1与位置3元素相同，都是a，不需要对比，就知道一定不匹配，故该次对比可以省略。因此，可以直接回溯到位置1不匹配时需要回溯的地方，即位置0。

按此思想，可以将next数组优化为nextval数组，从而更加省略了对比次数。

void nextval(SString T,int next[]){int nextval[T.length+1];nextval[1] = 0;for(int i=2;i<=T.length;i++){if(T.ch[i] == T.ch[next[i]]) nextval[i] = nextval[next[i]];else  nextval[i] = nextval[i];}
} int Index_KMP(SString S,SString T,int nextval){//和上面一样 
}