参照3GPP的标准文档，摘录其中下行共享信道与寻呼信道的LDPC编码流程，以便于进行对应的软件仿真

• 传输块加CRC校验

    记待传输的数据块序列为$a_0,a_1,\cdots ,a_{A-1}$，其中$A$为传输块的负载（payload）尺寸。加入CRC校验比特以提供检错能力，其中加入的CRC校验比特长度$L$由$A$的大小决定，如下式所示
  $$L=\{\begin{array}{l}24,ifA>3824\\ \\ 16,otherwise\end{array}$$
  对应选取的CRC生成多项式为
  $$\begin{gathered} g_{crc24a}(D)=D^{24}+D^{23}+D^{18}+D^{17}+D^{14}+D^{11}+D^{10}+D^7+D^6+D^5+D^4+D^3+D+1 \\ {g}_{crc16}(D)=D^{16}+D^{12}+D^5+1 \end{gathered}$$
  生成的校验比特序列$p_0,p_1,\cdots ,p_{L-1}$附在数据块序列后，记加了CRC校验的序列为$b_0,b_1,\cdots ,b_{B-1}$，即有
  $$\{\begin{array}{l}{b}_k=a_k,0\le k<A\\ \\ b_k=p_{k-A},A\le k<B\end{array}$$
  其中$B=A+L$。

• 选择基图BG

  根据具体传输要求决定的码率$R$，以及传输块原始的长度$A$，确定基图的选择如下
  $$BG=\{\begin{array}{l}BG2,ifA\le 292or\{\begin{array}{l}A\le 3824\\ R\le 0.67\end{array}orR\le 0.25\\ \\ BG1,otherwise\end{array}$$

• 传输块分段

  对应于不同的基图，单次能够传输的码块大小是有限制的，记码块最大为$B_{max}$，则有
  $$B_{max}=\{\begin{array}{l}8448,ifBG1\\ \\ 3840,ifBG2\end{array}$$
  如果传输块尺寸$B>B_{max}$，则要求对传输块进行分块，并且每个分块还要附加长度$L^{{}^{\prime }}=24$的CRC校验比特，综上所述，所需分块的数目$C$和分块后总体传输块大小$B^{{}^{\prime }}$的计算如下
  $$\begin{array}{rl}C& =\{\begin{array}{l}1,ifB\le B_{max}\\ \\ \lceil B/(B_{max}-L^{{}^{\prime }})\rceil ,otherwise\end{array}\\ & \\ B^{{}^{\prime }}& =\{\begin{array}{l}B,ifB\le B_{max}\\ \\ B+C\cdot L^{{}^{\prime }},otherwise\end{array}\end{array}$$

• 确定码块大小

    由于标准中支持的提升值$Z$肯定不可能是连续的，因此用校验矩阵进行编码时支持的输入比特序列长度也不会是连续的。如果直接将传输块均分，得到的码块长度很可能不会恰好满足校验矩阵对编码序列长度的要求，需要填充比特才行。另外，标准中的BG2还要求根据输入码块长度来适当删减对应的核心矩阵系统列，这也会影响到最终编码码块长度的确定。所以，综合来看，码块长度的确定还需要进行对应的计算.

    设对传输块$B^{{}^{\prime }}$均分得到的码块长度为$K^{{}^{\prime }}$，则有
  $$K^{{}^{\prime }}=\frac{B^{{}^{\prime }}}{C}$$
  另外，编码对应系统列数$K_b$确定如下
  $$K_b=\begin{array}{r}\{\begin{array}{ll}22,& BG1\\ & \\ 10,& BG2\&\&B>640\\ & \\ 9,& BG2\&\&640\ge B>560\\ & \\ 8,& BG2\&\&560\ge B>192\\ & \\ 6,& BG2\&\&B\le 192\end{array}\end{array}$$
  根据式子$Z_c\ge K^{{}^{\prime }}/K_b$，确定满足这一条件的最小提升值$Z$，其可能取值如下所示
  Z = a ⋅ 2 i , a = { 2 , 3 , 5 , 7 , 9 , 11 , 13 , 15 } , i = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 } , Z ≤ 384 Z=a·2^i,\ a=\{2,3,5,7,9,11,13,15\},\ i=\{0,1,2,3,4,5,6,7\},Z\leq384 Z=a⋅2i, a={2,3,5,7,9,11,13,15}, i={0,1,2,3,4,5,6,7},Z≤384

  最终确定编码码块的大小$K$如下
  $$K=\begin{array}{r}\{\begin{array}{ll}22Z_c,& BG1\\ & \\ 10Z_c,& BG2\end{array}\end{array}$$

• 码块填充比特

    确定了编码码块的大小后，还需要确定编码码块的组成。若码块$C=1$，则只需要在信息块$B^{{}^{\prime }}$后添加填充比特$<NULL>(0)$即可，此时的编码码块组成如下

  

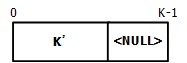
  若码块数$C>1$，则需要添加长度$L=24$的CRC校验比特，其生成多项式如下所示
  $$g_{crc24b}(D)=D^{24}+D^{23}+D^6+D^5+D+1$$
  此时的码块组成如下所示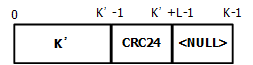

  

• LDPC编码

    确定了编码码块后，要进行编码，还需要得到校验矩阵。具体来说，标准中根据基图和提升值所属组确定了$2\times 8=16$个校验矩阵，其中提升值所属组即计算式$Z=a\cdot 2^i$中的$a$，共8种取值即8组。另外，这16个校验矩阵的移位值是按照对应提升值组中的最大值确定的，若要应用到当前编码中则需要对移位值进行$Z_c$的求余，这样得到的计算结果才是当前提升值对应的移位值。

    通过编码码块和校验矩阵进行编码后，根据基图的不同，得到的系统编码比特序列长$N^{{}^{\prime }}$为
  $$N^{{}^{\prime }}=\begin{array}{r}\{\begin{array}{ll}68Z_c,& BG1\\ & \\ 52Z_c,& BG2\end{array}\end{array}$$
  值得注意的是，5G NR所采用的基图在设计时给前$2Z_c$个系统比特对应的两列设置了较大的列重，使得发送端将这两列对应的系统比特打掉后仍然能够在接收端较大可能地恢复出来。而打掉这$2Z_c$个系统比特后，可以对应地补上$2Z_c$个校验比特，以实现发送比特数不变的前提下性能上的提升。因此，虽然标准中给的最终编码后序列长度$N=66Z_c$或$N=50Z_c$，但是实际仿真中还是会在后面补上校验比特的。