摘要

近年来，多跳知识图(KG)推理得到了广泛的研究，以提供具有证据路径的缺失链接的可解释预测。大多数先前的工作使用基于强化学习(RL)的方法来学习导航到目标实体的路径。然而，这些方法的收敛速度慢，收敛性差，当路径上有一条缺失边时，它们可能无法推断出某条路径。在这里，我们介绍了第一个基于序列到序列的多跳推理框架SQUIRE，它利用编码器-解码器Transformer结构将查询转换为路径。我们的框架带来了两个好处:(1)它可以以端到端方式学习和预测，这使得收敛更快更好;(2)我们的变压器模型不依赖于现有的边缘来生成路径，并且具有沿路径补全缺失边缘的灵活性，特别是在稀疏KGs中。在标准KGs和稀疏KGs上的实验表明，我们的方法比之前的方法有了显著的改进，收敛速度提高了4 × 7倍。

 图1:不完全知识图中的多跳推理示例。缺失的链接(虚线箭头)可以从现有链接(实线箭头)推断出来。但是，当路径上有一条缺失的边(灰色虚线箭头)时，可能无法推断出这样的证据路径。

1.介绍

知识图(KG)以三元组的形式提供了关于现实世界中实体和关系的结构性知识。图中的每条边，用一个关系连接两个实体，表示一个三重事实(h;r;t).知识图谱支持各种下游任务，如问答(Hao et al .， 2017)、信息检索(Xiong et al .， 2017a)和分层推理(Bai et al .， 2021)。然而，实际的KG往往存在不完备性，因此提出了KG完备性的任务，如预测给定(h;r)。应对此类挑战的一种流行方法是知识图嵌入(KGE) (Bordes等人，2013;Dettmers等人，2018)，以完整的黑盒方式推断缺失边缘。

为了加强KG完成的可解释性，(Das et al .， 2018)提出了多跳知识图推理。给定一个三重查询(h;r)，任务的目的不仅是预测尾实体t，而是给出从h到t表示推理过程的证据路径，例如，我们可以从“出生”和“语言”的关系路径中推断(Albert, native language， ?)，如图1所示。

以前的大多数作品使用基于步行的方法(Das等人，2018;Lin等人，2018;Lv等人，2019;Lei et al .， 2020)来解决这一问题，其中在强化学习(RL)框架下训练智能体学习从头部实体“行走”到尾部实体。这些基于强化学习的方法的一个主要缺点是它们的收敛速度慢且较差，因为在强化学习的训练过程中，奖励可能会暂时延迟(Woergoetter和Porr, 2008)。在图2中，我们展示了KGE模型(TransE by Bordes et al .(2013)，蓝色曲线)和基于rl的多跳推理模型(MultiHopKG by Lin et al .(2018)，棕色曲线)在不同图大小下的训练时间。

虽然多跳推理是一个比KG完成更难的任务，但对于基于rl的模型，随着图的大小增长，时间上的权衡仍然是难以忍受的。此外，正如Lv et al(2020)所指出的，以往的方法存在路径缺失问题，即由于路径沿线缺少边，模型无法推断出一对实体之间的证据路径，特别是在稀疏的KGs中。如图1所示，Albert和Hans之间由于缺少关系“spouse”而没有证据路径。

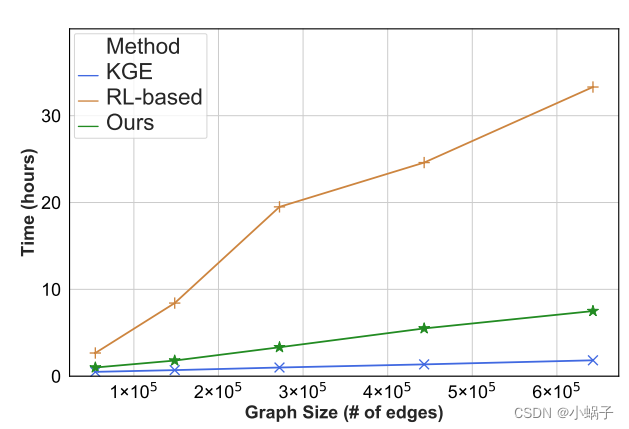
图2:KGE模型、基于rl的多跳推理模型和我们的多跳推理模型在不同图大小(以边数衡量)下的训练时间(单位小时)。

令人惊讶的是，我们证明了这两个缺点都可以通过一个新的序列到序列的多跳推理框架(SQUIRE)来缓解。通过将多跳推理作为序列到序列的问题，我们使用Transformer编码器-解码器模型(Vaswani等人，2017)将查询序列“翻译”为路径序列。

对于模型学习，每个三元组诱导一个由源序列组成的监督训练样本，即query (h;r)，以及从h和t之间的所有路径中采样的目标路径序列。因此，SQUIRE框架以完整的端到端方式学习和预测，比基于rl的方法更快、更稳定的收敛(训练时间对比图2中的绿色曲线)。此外，我们的方法自然地克服了路径缺失问题，因为Transformer不明确地依赖于图中的现有边来生成路径序列。也就是说，我们提出的方法具有“步行完成”的灵活性:自动推断路径上的缺失边缘。

同时，多跳推理对我们的框架提出了特殊的挑战。(a)噪声样本:不像在语言建模中，我们有一个真实的目标序列，在我们的例子中，在目标路径上没有这样的监督。获得目标路径的一种朴素方法是从h和t之间的所有路径中随机采样，但这可能会给模型学习引入噪声，因为随机路径可能是假的。为了解决这个问题，我们提出了规则增强学习。我们通过从KG中挖掘的逻辑规则来搜索基真路径，与随机采样路径相比，这些规则噪声更小，更可靠。(b)历史间隙:在训练过程中，我们为模型预测下一个token提供了groundtruth序列作为路径历史。然而，在推理过程中，历史是由模型从头生成的，导致其偏离训练分布。在语言建模中，这也被称为暴露偏差(Ranzato等人，2016)，这是自回归模型面临的一个常见挑战。为了缩小这种差距，我们提出了迭代训练，该训练基于模型先前的预测迭代地将新路径聚合到训练集，使模型适应它诱导的历史标记的分布。

2.相关工作

2.1 Knowledge Graph Embedding

知识图嵌入(KGE)方法将实体映射到低维嵌入空间中的向量，并将关系建模为实体嵌入之间的转换。突出的例子包括TransE (Bordes等人，2013)、ConvE (Dettmers等人，2018)、RotatE (Sun等人，2018)和TuckER (Balaževic等人，2019)。这些模型中的每一个都配备了一个评分函数，该函数将任何三组映射到一个标量分数，该分数测量三组的可能性。实体和关系的嵌入是通过优化评分函数来学习的，使得真三元组的似然得分高，假三元组的似然得分低。

2.2 Multi-hop Reasoning

多跳推理的目的不仅是找到查询的目标实体(h;r;?)，还有从h到t的推理路径来支持预测。

DeepPath (Xiong et al .， 2017b)是第一个采用RL框架进行多跳推理的方法。在这项工作之后，MINERVA (Das et al .， 2018)将强化算法引入到该任务中。考虑到不完整的KG环境可能会给出低质量的奖励，MultiHopKG (Lin等人，2018)提出了一个预训练的KGE模型的奖励塑造。DacKGR (Lv等，2020)进一步在稀疏KGs中应用了动态预测和补全。

除了上述基于rl的方法外，还提出了几种基于符号规则的模型来提高KG完成的可解释性，包括NTP (Rocktäschel and Riedel, 2017)、NeuralLP (Yang等人，2017)和AnyBURL (Meilicke等人，2019)。这些方法中的大多数都是从自动学习的逻辑规则中提供证据，在某种程度上，这些方法的可解释性比基于rl的方法更弱，后者提供证据路径。

2.3 Reinforcement Learning via Transformer

有趣的是，最近的作品(Chen et al, 2021;Janner等人，2021)已经证明了将RL视为序列建模问题的可行性。他们使用Transformer对包括状态、动作和奖励在内的轨迹进行建模，并且他们的架构在离线RL任务上实现了有希望的结果。在我们的多跳推理任务中，这些发现表明有可能用Transformer取代以前的RL管道

3. Methodology

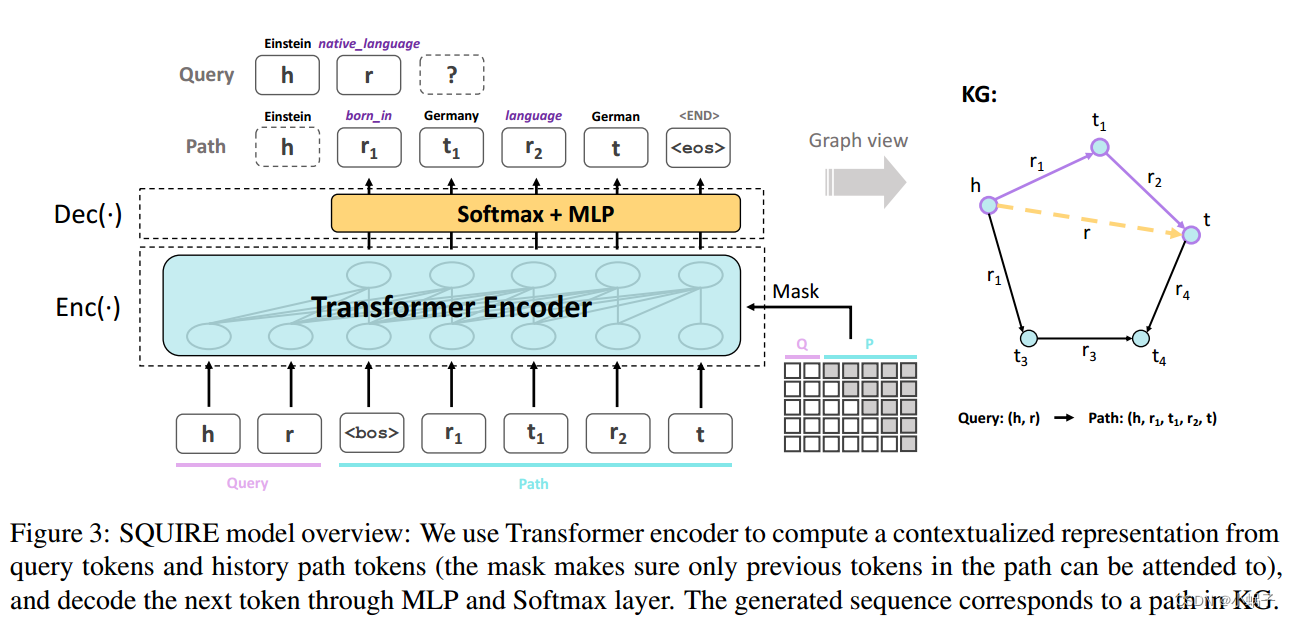
图3:SQUIRE模型概述:我们使用Transformer编码器从查询令牌和历史路径令牌计算上下文化表示(掩码确保路径中只有前一个令牌可以被关注)，并通过MLP和Softmax层解码下一个令牌。生成的序列对应于KG中的路径。

3.1 Preliminaries

 3.2 SQUIRE Framework

我们的端到端SQUIRE方法将多跳推理框架为序列到序列的任务。查询被视为源序列，路径被视为目标序列。如图3所示，我们利用Transformer编码器将查询和以前的路径序列映射到上下文化的表示，并进一步使用这种表示对输出路径进行逐个标记的自回归解码。

我们的框架背后的直觉很简单:多跳推理任务设置类似于NLP中的问答任务:不同的实体和关系可以被解释为不同的单词，其上下文嵌入可以从图中的边缘学习。此外，像(例如，“母语!可以从训练样本中学习，其中查询中的r被分解为r1r2在路径上。

 

我们的序列到序列框架带来了两个挑战。(a)噪声样本:注意，在训练过程中，我们从h到t的路径作为目标路径进行采样，因为“基础真理”推理路径没有黄金标准。这可能会导致低质量的路径，并在模型学习中引入噪声。(b)历史差距:训练过程中的历史路径令牌与推理过程中的历史路径令牌之间存在差距，前者来自于groundtruth数据分布，后者由模型诱导。

3.3 Rule-enhanced Learning

为了解决噪声样本的挑战，我们提出了规则增强学习，使用挖掘的规则来指导路径搜索并获得高质量的路径查询对。受到基于规则的多跳推理方法最新进展的启发(Yang et al .， 2017;Sadeghian等人，2019)，我们使用AnyBURL (Meilicke等人，2019)，这是在KG上进行规则挖掘的Sota方法，可以有效地挖掘逻辑规则。每条规则将单个关系分解为多个关系(包括逆关系)的组合每条规则都有一个置信度分数，我们选择置信度分数大于某个阈值的规则，并将其视为“黄金规则”。然后我们使用这些规则来找到h和t之间的证据路径。例如，如果关系r的一个规则是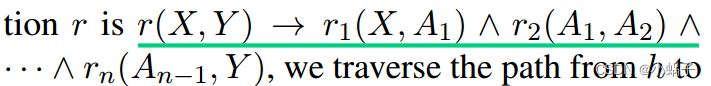如果没有一条规则导致图中的有效路径，我们通过随机抽样获得路径。

然而，利用基于规则的方法生成有效的查询路径对会引入规则噪声问题。这是因为一些关系规则并不适用于所有实体，并且可能导致某些实体从h到t的路径不合理。我们展示了一种迭代训练策略，在下一节详细阐述，可以缓解噪声规则问题。

3.4迭代训练

我们的历史差距挑战也是自回归模型(称为语言建模中的暴露偏差)中常见的问题，其中解决方案背后的核心思想(Venkatraman等人，2015;Zhang et al .， 2019)是在推理过程中训练模型在相同条件下进行预测。考虑到类似的直觉，我们提出了一种新的训练策略，该策略基于模型的预测迭代地聚合新的训练数据，以帮助模型适应其诱导的历史标记分布。我们的数据聚合思想受到DAgger算法的启发(Ross等人，2011)，该算法旨在提高RL在顺序预测问题中的性能。

我们的算法进行如下。在第一次迭代中，我们生成了如前所述的查询路径训练集U，并对模型进行了几个epoch的训练。在第k次迭代(k > 1)时，对于图中的每个triple，我们部分地利用当前模型来寻找路径，并向u中添加一个新的训练样本。具体来说，我们的算法使用当前模型来预测前(k−1)个跳数，并以最大长度n搜索这些令牌后面的路径。如果无法找到后续路径，可能是由于模型在预测前(k−1)个跳数时失败;然后我们再次搜索整个路径来加强模型在这个样本上的学习。在第k次迭代的数据聚合后，训练集的大小成为初始大小的k倍，我们在下一次迭代之前继续在新的训练集上训练模型进行相同步数的训练。迭代的总次数是N，这是路径的最大跳数。图1给出了详细的算法。

注意，在第k次迭代中，τ2是在τ1之后随机采样的，有人可能会担心这会给训练数据带来噪声。然而，由于模型在过去的迭代中学习了“软”规则，使得τ1比随机抽样更合理，那么留给τ2的搜索空间就更集中在groundtruth路径周围。

此外，迭代训练策略可以缓解规则增强学习带来的规则噪声问题。这些有噪声规则得到的路径可以在数据聚合步骤中被替换，同时，需要我们模型先前预测的路径可以作为更可靠的训练样本。