** 作者：刘兴禄， 清华大学，清华-伯克利深圳学院，博士在读**

证明绝对值线性化的等价性

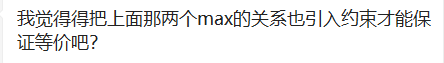
下面我们来证明一下绝对值转化的等价性：

命题：
z + = max ⁡ { 0 , z } ( 1 ) z − = max ⁡ { 0 , − z } ( 2 ) z^+=\max \left\{ 0,z \right\} \,\, \left( 1 \right) \\ z^-=\max \left\{ 0,-z \right\} \,\, \left( 2 \right) z+=max{0,z}(1)z−=max{0,−z}(2)
和
$$\begin{gathered} z=z^{+}-z^{-}\left(3\right) \\ |z|=z^{+}+z^{-}\left(4\right) \end{gathered}$$
互为充要条件。

证明：

充分性：根据(1)(2)，我们有
$$\begin{gathered} z=z^{+}-z^{-}\left(3\right) \\ |z|=z^{+}+z^{-}\left(4\right) \end{gathered}$$
充分性得证
必要性： 根据(3)(4)我们有
( 3 ) + ( 4 ) = z + ∣ z ∣ = 2 z + → z + = z + ∣ z ∣ 2 ( 3 ) − ( 4 ) = z − ∣ z ∣ = − 2 z − → z − = − z − ∣ z ∣ 2 情况一： i f z ⩾ 0 , z + = z + ∣ z ∣ 2 = z + z 2 = z = max ⁡ { 0 , z } z − = − z − ∣ z ∣ 2 = − z − z 2 = 0 = max ⁡ { 0 , − z } 情况二： i f z ⩽ 0 , z + = z + ∣ z ∣ 2 = z − z 2 = 0 = max ⁡ { 0 , z } z − = − z − ∣ z ∣ 2 = − z − ( − z ) 2 = − 2 z 2 = − z = max ⁡ { 0 , − z } \left( 3 \right) +\left( 4 \right) =z+|z|=2z^+\,\, \rightarrow \,\,z^+=\frac{z+|z|}{2} \\ \left( 3 \right) -\left( 4 \right) =z-|z|=-2z^-\,\, \rightarrow \,\,z^-=-\frac{z-|z|}{2} \\ \text{情况一：}if\,\,z\geqslant 0, z^+=\frac{z+|z|}{2}=\frac{z+z}{2}=z=\max \left\{ 0,z \right\} \\ z^-=-\frac{z-|z|}{2}=-\frac{z-z}{2}=0=\max \left\{ 0,-z \right\} \\ \text{情况二：}if\,\,z\leqslant 0, z^+=\frac{z+|z|}{2}=\frac{z-z}{2}=0=\max \left\{ 0,z \right\} \\ z^-=-\frac{z-|z|}{2}=-\frac{z-\left( -z \right)}{2}=-\frac{2z}{2}=-z=\max \left\{ 0,-z \right\} (3)+(4)=z+∣z∣=2z+→z+=2z+∣z∣​(3)−(4)=z−∣z∣=−2z−→z−=−2z−∣z∣​情况一：ifz⩾0,z+=2z+∣z∣​=2z+z​=z=max{0,z}z−=−2z−∣z∣​=−2z−z​=0=max{0,−z}情况二：ifz⩽0,z+=2z+∣z∣​=2z−z​=0=max{0,z}z−=−2z−∣z∣​=−2z−(−z)​=−22z​=−z=max{0,−z}
因此，必要性得证。

综上，(1)(2)和(3)(4)互为充要条件，以上转化完全等价。