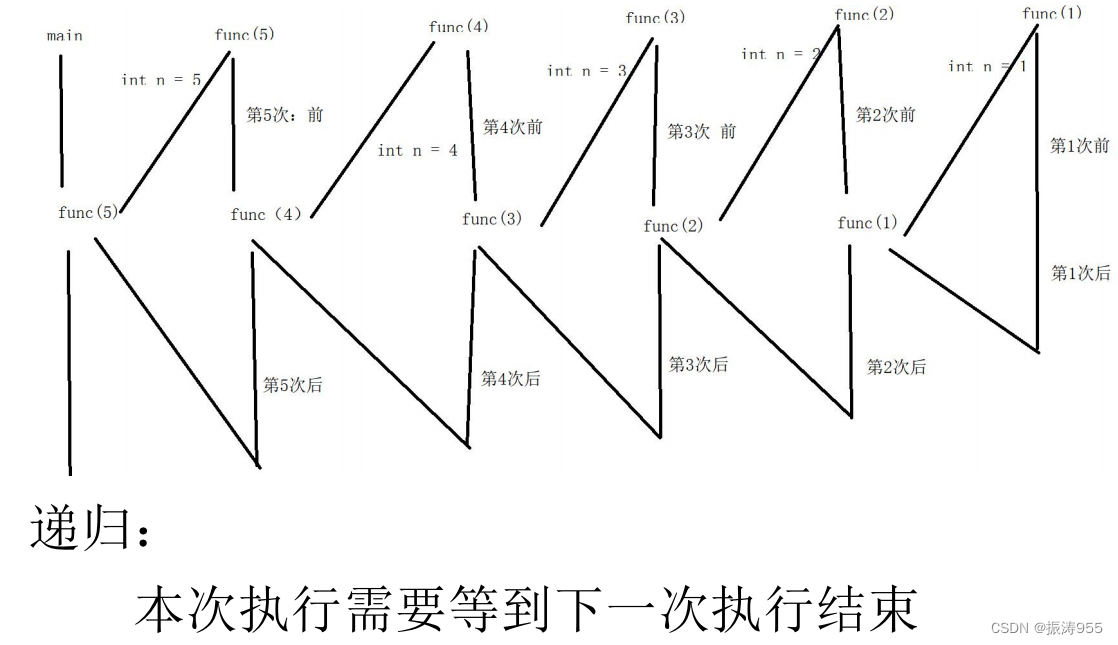
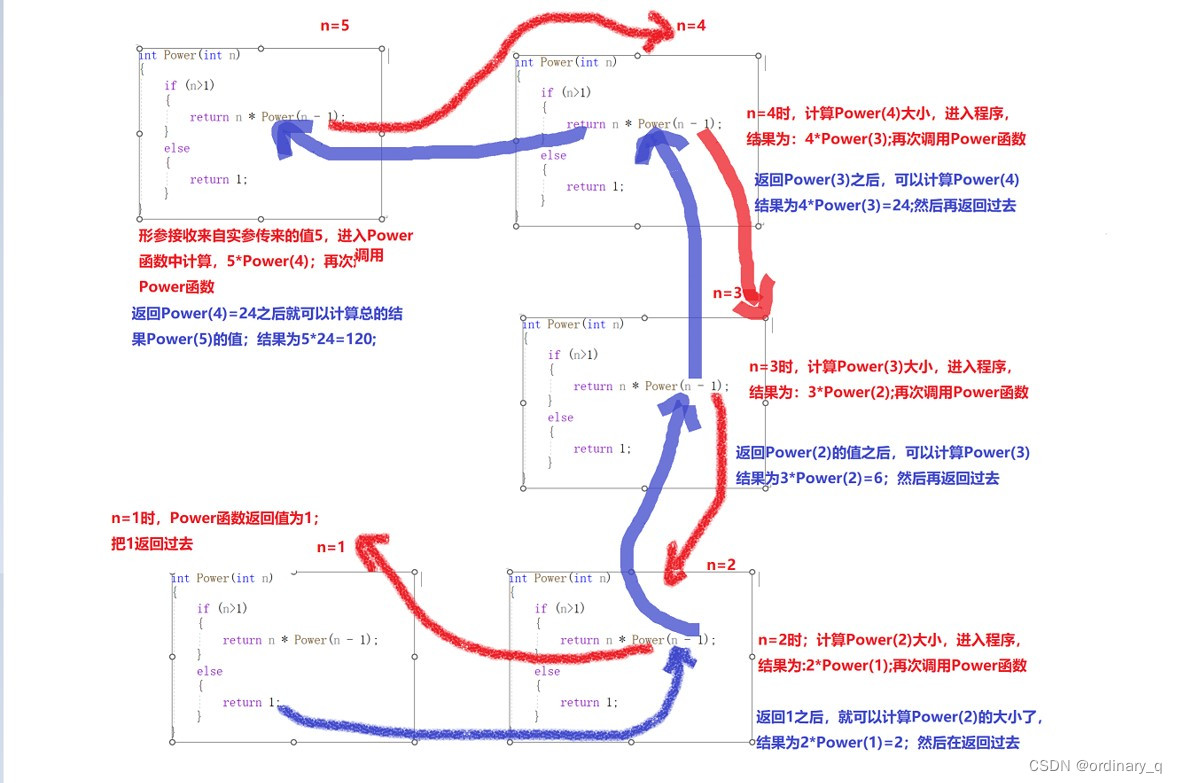
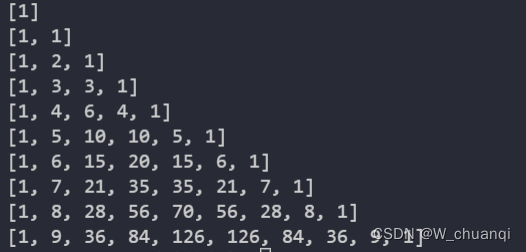
杨辉三角的概念
比较详细的知识可以看这里,在杨辉三角中,每个数是它左上方和右上方的数的和。

1/ \1 1/ \ / \1 2 1/ \ / \ / \1 3 3 1/ \ / \ / \ / \1 4 6 4 1/ \ / \ / \ / \ / \
1 5 10 10 5 1
解法1:动态规划
- 思路:
如果能够知道一行杨辉三角,我们就可以根据每对相邻的值轻松地计算出它的下一行。 - 解法:
首先,我们会生成整个 triangle 列表,三角形的每一行都以子列表的形式存储。然后,我们会检查行数为0的特殊情况,否则我们会返回[1]。如果行数大于1,那么我们用[1]作为第一行来初始化,所以可以得到如下程序:
def generate(num_rows):triangle = []for row_num in range(num_rows):# 初始化zhenghangsrow = [None for _ in range(row_num+1)]# 将第一个数和最后一个数设置为1row[0], row[-1] = 1, 1for j in range(1, len(row)-1):row[j] = triangle[row_num-1][j-1] + triangle[row_num-1][j]triangle.append(row)return triangle
解法2:生成器
本质上和解法1的思想一致,但是可以使用生成器来都程序进行改写,程序如下:
def generate(num_rows):def triangles():t = [1]while True:yield ts = [0] + tt = t + [0]for i in range(len(s)):t[i] = s[i] + t[i]result = []n = 0for t in triangles():result.append(t)n = n + 1if n == numRows:breakreturn result
但是奇怪的是,我将这个程序通过leetcode进行提交,却得到了超时的错误,按理说使用生成器进行操作应该是更快才是,但是反而慢了?不得其解,如果有了解的同学欢迎告知。
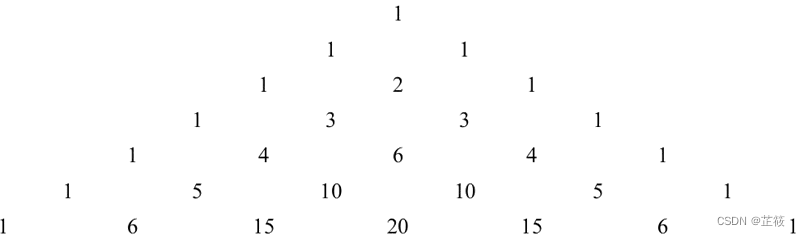
解法三:数学公式
运用杨辉三角的公式:第n行第m个数可表示为C(n-1,m-1) = (n - 1)!/(m - 1)!*(n - m - 2)!
from math import factorial as f def generate(num_rows):res = [[] for _ in range(numRows)] if not numRows: return [] for i in range(numRows): for j in range(i + 1): res[i].append(f(i)//(f(j)*f(i - j)))return res
在python中如果利用足够的python特性可以一行程序解决这个问题:
def generate(num_rows):return [[comb(i,j) for j in range(i+1)] for i in range(numRows)]
其中comb函数是python3.8 新引入的特性,主要是为了计算C(n, m),也就是从n中取出m个数的概率
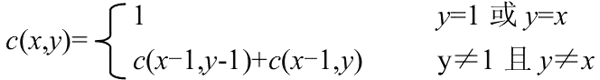



![[C语言] 函数:库函数--自定义函数--函数的调用--练习--详解<个人>------(1)](https://img-blog.csdnimg.cn/efa37cda89884278915de2c31b8c2d96.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA5bCP55m95Y-I6I-c,size_20,color_FFFFFF,t_70,g_se,x_16)