转自:https://blog.csdn.net/ting0922/article/details/83068800
在线性代数中,方阵A(n*n)的迹定义为主对角线元素的和。即:

矩阵的迹表示的是特征值的和,它不随基的变化而变化。通常,这种特性可以用来定义线性算子的轨迹。(注意:迹是对方阵而言的)
举例:
A是一个方阵,如下:
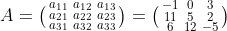
则A的迹表示为:
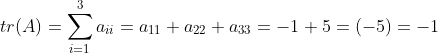
迹的特性:
- 迹是满足线性映射的,即:
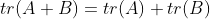
t r ( c ⋅ A ) = c ⋅ t r ( A ) tr(c\cdot{A})=c\cdot{tr(A)} tr(c⋅A)=c⋅tr(A)
其中A,B 是方阵,c是常数。
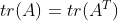
- 矩阵乘积的迹
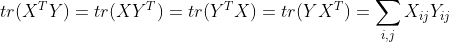
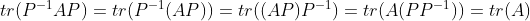
参考资料:
[1] 【机器学习】汇总详解:矩阵的迹以及迹对矩阵求导 2018.5
[2] 矩阵的迹(Trace)2018.10