堆的定义:
n个关键字序列K[1....n]称为堆,当且仅当改序列满足:

第一种为:小根堆:每个结点的值都小于或等于左右孩子结点

第二种为:大根堆:每个结点的值都大于或等于左右孩子结点

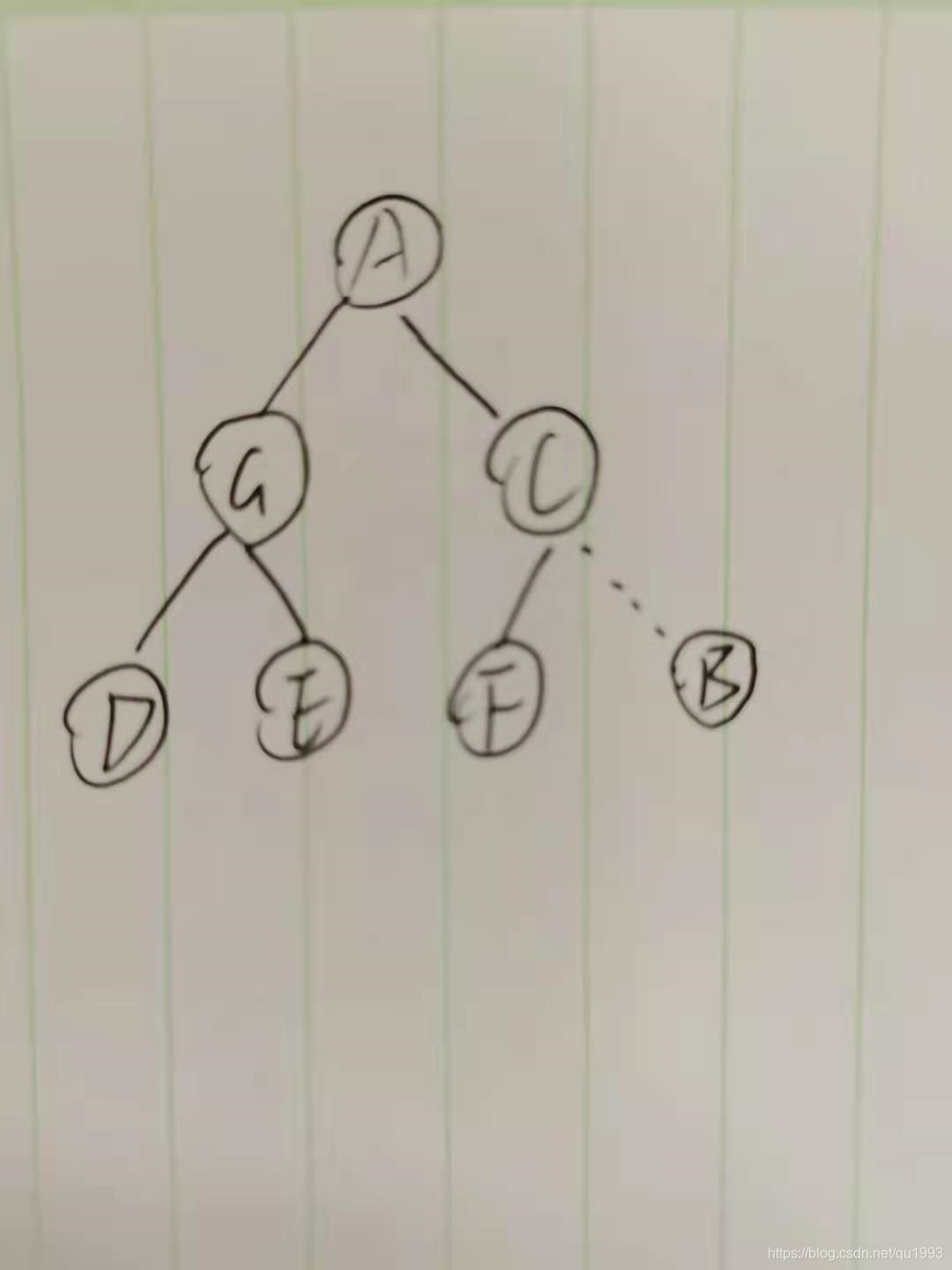
堆是一种完全二叉树。完全二叉树 是 一种除了最后一层之外的其他每一层都被完全填充,并且所有结点都保持向左对齐的树,向左对齐指的是:

堆排序:
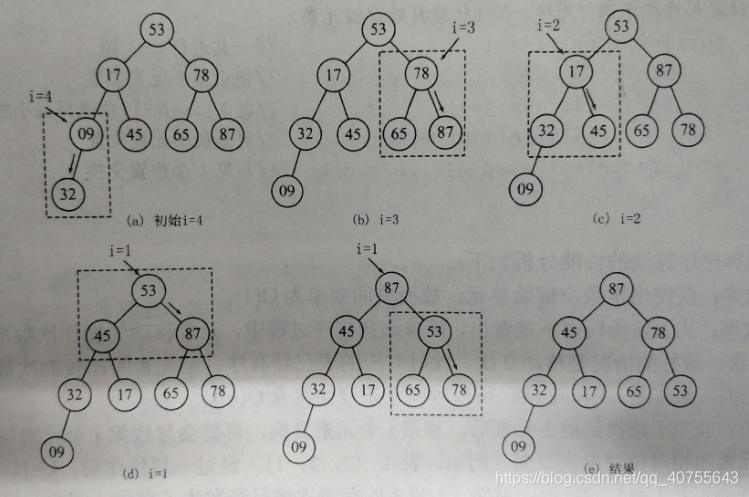
堆排序的关键是构造初始堆。对初始序列构建堆,就是一个反复筛选的过程。
N个节点的完全二叉树,最后一个节点是第[N//2]个节点的孩子。
对第[N//2]个节点为根的子树进行筛选(对于大根堆):若根节点的关键字小于左右子树中关键字的较大者,则交换,使该子树成为堆。
接着,由后向前依次对各节点([n//2]-1~1)为根的子树进行筛选,看该节点是否大于其左右子树的值,若不是,将左右子树节点中较大值与之交换。
代码:
import randomdef sift(data, root, end):#temp = rootwhile True:max_child = root * 2 +1 #最大子树索引先赋给左子树if max_child > end:breakif max_child+1 <= end and data[max_child] < data[max_child+1]: #右子树的关键字大于左子树max_child += 1 #最大子树索引赋给右子树if data[root] < data[max_child]: #最大子树的关键字大于根节点data[root], data[max_child] = data[max_child], data[root] #交换这两个数root = max_child #修改根节点的索引else:breakdef heap_sort(data):n = len(data)#创建大根堆for root in range(n//2,-1,-1):sift(data,root,n-1)#堆排序,堆顶元素和堆末尾的元素交换,然后把剩下的元素调整为一个大根堆for end in range(n-1, -1, -1):data[0], data[end] = data[end], data[0]sift(data,0,end-1)if __name__ == "__main__":li = list(range(10))random.shuffle(li)print(li)heap_sort(li)print(li)