对归一化和标准化有疑惑，整理了Z-score和mapminmax的用法区分，参考链接放在文末。

function data = normlization(data, choose)

数据归一化函数可以包含：不归一化，z-score标准化，最大最小归一化

function data = normlization(data, choose)
% 数据归一化
if choose==0% 不归一化data = data;elseif choose==1% Z-score归一化（标准化）data = bsxfun(@minus, data, mean(data));data = bsxfun(@rdivide, data, std(data));elseif choose==2% 最大-最小归一化处理% ones(data_num,1)         % 构成一个data_num行1列的向量，里面每个元素都是1% min(data)                  % 构成包含每一列的最小值的行向量，1行n列% (data-ones(data_num,1)*min(data))    % 让数据中的每个元素减去该元素对应列计算出的均值[data_num,n]=size(data);data=(data-ones(data_num,1)*min(data))./(ones(data_num,1)*(max(data)-min(data)));
end
end

注意：可以在elseif后面添加自己的方法。

最大最小归一化，顾名思义，就是利用数据列中的最大值和最小值进行标准化处理，标准化后的数值处于[0,1]之间，计算方式为数据与该列的最小值作差，再除以极差。

具体公式为：

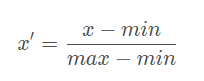
其中，x’表示单个数据的取值，min是数据所在列的最小值，max是数据所在列的最大值。

mapminmax 归一化

mapminmax()函数是Matlab自带的函数，主要用来对数据进行归一化处理。它把所有的数据都转换为[-1,1](默认，可自己设定)之间的数，目的就是取消各维数据间的数量别差别，防止大数吃小数。

不同变量往往量纲不同，归一化可以消除量纲对最终结果的影响，使不同变量具有可比性。在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用归一化方法。

矩阵归一化：

Y=mapminmax(A,ymin,ymax);    % 默认ymin = -1,ymax =1,缩放至 [0,1]

默认：

按行缩放，默认范围[-1,1]（ymin = -1，ymax = 1）。
Y是归一化后的矩阵。

原理：y = (ymax-ymin)*(x-xmin)/(xmax-xmin) + ymin

Y=mapminmax(A,0,1); %指定X每行缩放到[0，1]

注意：当X的一行中，若xmin和xmax相等，那么分母xmax-xmin为零，mapminmax对当前行不处理。输出仍为原始行数据。

例子：

mapminmax的归一化与反归一化用法等可见主页(3条消息) y = mapminmax(‘apply‘,x,ps)与mapminmax(‘reverse‘,y,ps)_FDA_sq的博客-CSDN博客

zscore 标准化

z-score标准化方法适用于属性A的最大值和最小值未知的情况。数据标准化后均值为0，方差为1。

新数据=（原数据-均值）/标准差：

(A - mean(A))./std(A)

等同于bsxfun的使用（从矩阵 A 的对应列元素中减去列均值。然后，按标准差进行归一化。）

C = bsxfun(@minus, A, mean(A));
D = bsxfun(@rdivide, C, std(A))

默认：

按列缩放，输出的矩阵Y每列服从正态分布，每列的均值是0，标准差是1
如果某一列数据全相等，标准化的结果为 0(向量)

使用方法：

Z = zscore(X,flag,dim)

flag: 使用由flag表示的标准偏差缩放X。

-- 如果flag为0(默认)，则zscore使用样本标准偏差缩放X，标准偏差公式的分母为n - 1。zscore(X,0)与zscore(X)相同。

-- 如果flag为1，则zscore使用总体标准差对X进行缩放，n是标准差公式的分母。

dim: 对于矩阵X，如果dim = 1(默认)，则zscore使用沿X列的均值和标准差，如果dim = 2，则zscore使用沿X行的均值和标准差。

[Y,mean,std]=zscore(X)  %X：n*d;Y是标准化后矩阵，mean和std分别是原数据每列的平均值和标准差

举例：

>> a=[1,2,3;4,5,6];
>> b=zscore(a)
b =-0.7071   -0.7071   -0.70710.7071    0.7071    0.7071% 验证标准化后的矩阵每列均值为0，标准差为1
>> std(b)                
ans =1     1     1
>> mean(b)
ans =0     0     0

二者区别

如果对输出结果范围有要求，用归一化如果数据较为稳定，不存在极端的最大最小值，用归一化如果数据存在异常值和较多噪音，用标准化，可以间接通过中心化避免异常值和极端值的影响

神经网络使用归一化的原因

我们在对输⼊数据做标准化处理：处理后的任意⼀个特征在数据集中所有样本上的均值为0、标准差为1。标准化处理输⼊数据使各个特征的分布相近：这往往更容易训练出有效的模型。通常来说，数据标准化预处理对于浅层模型就⾜够有效了。随着模型训练的进⾏，当每层中参数更新时，靠近输出层的输出较难出现剧烈变化。

但对深层神经⽹络来说，即使输⼊数据已做标准化，训练中模型参数的更新依然很容易造成靠近输出层输出的剧烈变化。这种计算数值的不稳定性通常令我们难以训练出有效的深度模型。批量归⼀化(BatchNormalization)的提出正是为了应对深度模型训练的挑战。在模型训练时，批量归⼀化利⽤⼩批量上的均值和标准差，不断调整神经⽹络中间输出，从⽽使整个神经⽹络在各层的中间输出的数值更稳定。在模型训练时，在应用激活函数之前，先对一个层的输出进行归一化，将所有批数据强制在统一的数据分布下，然后再将其输入到下一层，使整个神经网络在各层的中间输出的数值更稳定。从而使深层神经网络更容易收敛而且降低模型过拟合的风险。

在卷积神经网络中卷积层和全连接层都可以使用批量归一化。对于卷积层，它的位置是在卷积计算之后、激活函数之前。对于全连接层，它是在仿射变换之后，激活函数之前。

参数解释

1.均值

mean(A): 如果A是一个向量，mean(A)返回A中元素的平均值; 如果A是一个矩阵，mean(A)将其中的各列视为向量，把矩阵中的每列看成一个向量，返回一个包含每一列所有元素的平均值的行向量；如果A是一个多元数组，mean(A)将数组中第一个非单一维的值看成一个向量，返回每个向量的平均值。

M = mean(A,dim)：返回A中沿着标量dim指定的维数上的元素的平均值。对于矩阵，mean(A,2)就是包含每一行的平均值的列向量。

mean(A,2): 返回值为该矩阵的各行向量的均值

mean(A,3): 返回矩阵本身（第三维，例如RGB图像三个通道）

>> A = [1 2 3; 3 3 6; 4 6 8; 4 7 7]
A =1     2     33     3     64     6     84     7     7
>> mean(A)
ans =3.0000    4.5000    6.0000>> mean(A,2)
ans =2466>> mean(A,3)
ans =1     2     33     3     64     6     84     7     7

2.标准差

标准差的两种计算公式如下：

(1）std(A，flag，dim):

std(A)函数求解的是最常见的标准差，此时除以的是N-1(std的默认格式是std(x,0,1))。

flag代表的是用哪一个标准差函数，如果取0，则代表除以N-1，如果是1代表的是除以N，
flag==0.........是除以n－1
flag==1.........是除以n
dim表示维数，是按照列求标准差还是按照行求标准差
dim==1..........是按照列分
dim==2..........是按照行分若是三维的矩阵，dim=＝3就按照第三维来分数据

注意：此函数命令不能对矩阵求整体的标准差，只能按照行或者列进行逐个求解标准差，默认情况下是按照列。

举例：

在MATLAB主窗口中输入std(A) 回车，结果如下：输出的是每一列的标准差。

>> A=[1 2 3;1 1 1 ]
A =1     2     31     1     1>> std(A)
ans =0    0.7071    1.4142

在MATLAB主窗口中输入如下命令：std(A,1,1) 敲回车 std(A,1,2) 敲回车,可以看到如下结果：

3. 最小值min

M = min(A) 返回数组的最小元素。

如果 A 是向量，则 min(A) 返回 A 的最小值。
如果 A 为矩阵，则 min(A) 是包含每一列的最小值的行向量。
如果 A 是多维数组，则 min(A) 沿大小不等于 1 的第一个数组维度计算，并将这些元素视为向量。此维度的大小将变为 1，而所有其他维度的大小保持不变。如果 A 是第一个维度为 0 的空数组，则 min(A) 返回与 A 大小相同的空数组。