什么是八皇后问题：

八皇后问题，是一个古老而著名的问题，是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。计算机发明后，有多种计算机语言可以解决此问题。

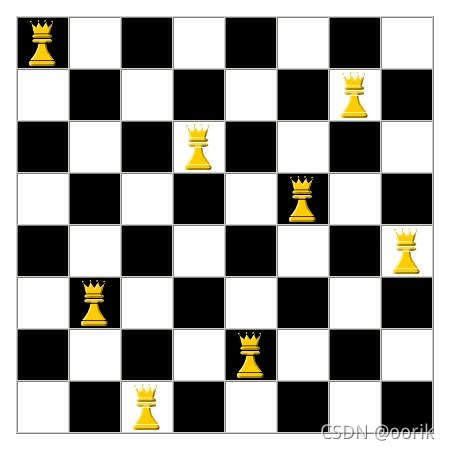
PS:这篇文章想法思路简单，代码量长，适合初学者学习，能更好的的理解这个问题

一、思路分析

首先我们思考一下，我们是应该一个一个的放置皇后还是该先把八个皇后全部放入棋盘然后在进行移动操作？我们是应该一个一个的放置皇后的。所谓牵一发而动全身，当八个皇后全部放入棋盘后，我们每移动一个皇后就会导致其他皇后的位置都得移动，从而导致了运算过程的冗杂重复，也导致了计算时间的增加和内存的浪费，对于追求效率的C语言来说这是不可取的，所以我们选择一个一个的放置皇后。
这样操作有什么优点呢？每当我们在选择移动一个皇后的位置的时候，其它已经放置好了的皇后的位置是不需要移动的，如果当某个皇后在属于它的行都不满足条件时，我们才需要回溯过去改变上一个皇后的位置。我们需要的就是循环的进行回溯操作，直到所有的皇后都放置完成，这样计算机的每一步操作都是有用的，不再是无用功。

我们来看一下回溯法：

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

二、代码实现过程

1.定义阶段

对于一个8*8的棋盘，我们很多人都会第一时间想到初始化一个二维数组来保存这个棋盘。但其实没有必要。因为八个皇后每一行只能有一个占据东宫的位置，所以我们只需要定义一个一维数组，每一个数字来表示皇后所在的列数即可。

2.皇后的摆放

我们首先要定义一个计数器，来记录每一次成功的8位皇后摆放方法

int count=0；

然后我们先摆放第一个皇后，再摆放第二个皇后的时候需要考虑
皇后与皇后不会再同一行上，不会在直角线上（成45°或135°）（定义的一维数组已经保证每一行只会有一个皇后）。所以我们在每摆放一个新的皇后时都要与前面的皇后进行if语句的判断

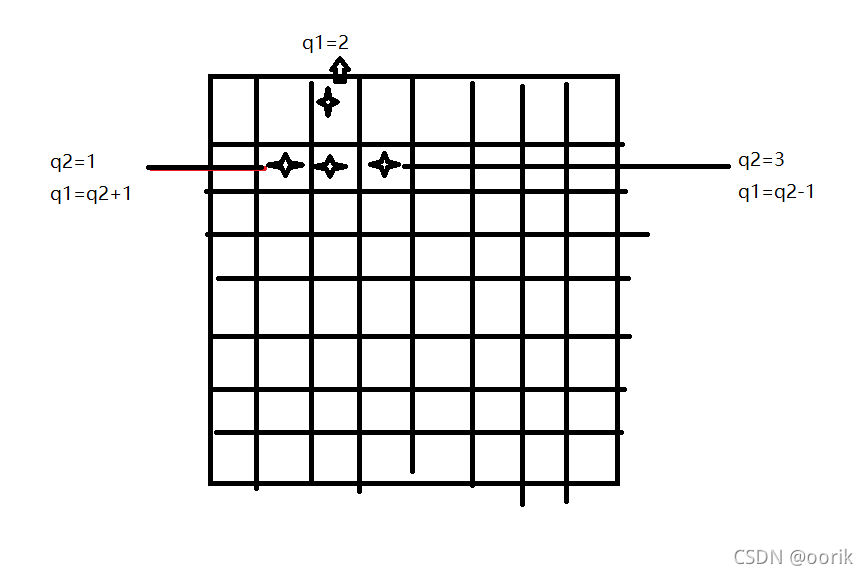
for (int q1 = 0; q1 < 8; q1++)  //第一个皇后{for (int q2 = 0; q2 < 8; q2++) //第二个皇后{if (q1 == q2 || q1 == q2 + 1 || q1 == q2 - 1) //不在同一列，不成对角线{continue;}}}

同理：在摆放第三个皇后的时候需要与第一个第二个皇后进行比较判断

	for (int q1 = 0; q1 < 8; q1++){for (int q2 = 0; q2 < 8; q2++){if (q1 == q2 || q1 == q2 + 1 || q1 == q2 - 1){continue;}for (int q3 = 0;q3 < 8; q3++){if (q1 == q3 || q1 == q3 + 2 || q1 == q3-2|| q2 == q3 || q2 == q3 + 1|| q2 == q3 - 1){continue;}}}}

continue如果if不成立那么返回上一层循环，对于上一个皇后的位置重新选择

可以按照上面思路自己写一写！

最后奉上完整版代码和实现 :

int main()
{int count = 0;//计数器for (int q1 = 0; q1 < 8; q1++){for (int q2 = 0; q2 < 8; q2++){if (q1 == q2 || q1 == q2 + 1 || q1 == q2 - 1){continue;}for (int q3 = 0;q3 < 8; q3++){if (q1 == q3 || q1 == q3 + 2 || q1 == q3-2|| q2 == q3 || q2 == q3 + 1|| q2 == q3 - 1){continue;}for (int q4 = 0; q4 < 8; q4++){if (q1 == q4 || q1 == q4 + 3 || q1 == q4 - 3 || q2 == q4 || q2 == q4 + 2|| q2 == q4- 2 || q3 == q4 || q3 == q4 + 1 || q3== q4- 1){continue;}for (int q5 = 0; q5 < 8; q5++){if (q1 == q5 || q1 == q5 + 4 || q1 == q5 - 4 || q2 == q5 || q2 == q5 + 3|| q2 == q5 - 3 || q3 == q5 || q3 == q5 + 2 || q3 == q5- 2 || q4 == q5 || q4 == q5 + 1 || q4 == q5 - 1){continue;}for (int q6 = 0; q6 < 8; q6++){if (q1 == q6 || q1 == q6 + 5 || q1 == q6 - 5|| q2 == q6 || q2 == q6 + 4 || q2 == q6 - 4|| q3 == q6 || q3 == q6 + 3 || q3 == q6 - 3|| q4 == q6 || q4 == q6 + 2 || q4 == q6 - 2|| q5 == q6 || q5 == q6 + 1 || q5 == q6 - 1){continue;}for (int q7 = 0; q7 < 8; q7++){if (q1 == q7 || q1 == q7 + 6 || q1 == q7 - 6|| q2 == q7 || q2 == q7 + 5 || q2 == q7 - 5|| q3 == q7 || q3 == q7 + 4 || q3 == q7 - 4|| q4 == q7 || q4 == q7 + 3 || q4 == q7 - 3|| q5 == q7 || q5 == q7 + 2 || q5 == q7 - 2|| q6 == q7 || q6 == q7 + 1 || q6 == q7 - 1){continue;}for (int q8 = 0; q8 < 8; q8++){if (q1 == q8 || q1 == q8 + 7 || q1 == q8 - 7|| q2 == q8 || q2 == q8 + 6 || q2 == q8 - 6|| q3 == q8 || q3 == q8 + 5 || q3 == q8 - 5|| q4 == q8 || q4 == q8 + 4 || q4 == q8 - 4|| q5 == q8 || q5 == q8 + 3 || q5 == q8 - 3|| q6 == q8 || q6 == q8 + 2 || q6 == q8 - 2|| q7 == q8 || q7 == q8 + 1 || q7 == q8 - 1){continue;}count++;printf("%d,%d,%d,%d,%d,%d,%d,%d\n", q1, q2, q3, q4,q5, q6, q7, q8);                        }}}}}}}}printf("一共有%d种方法", count);return 0;
}