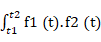独立$\Rightarrow$不相关

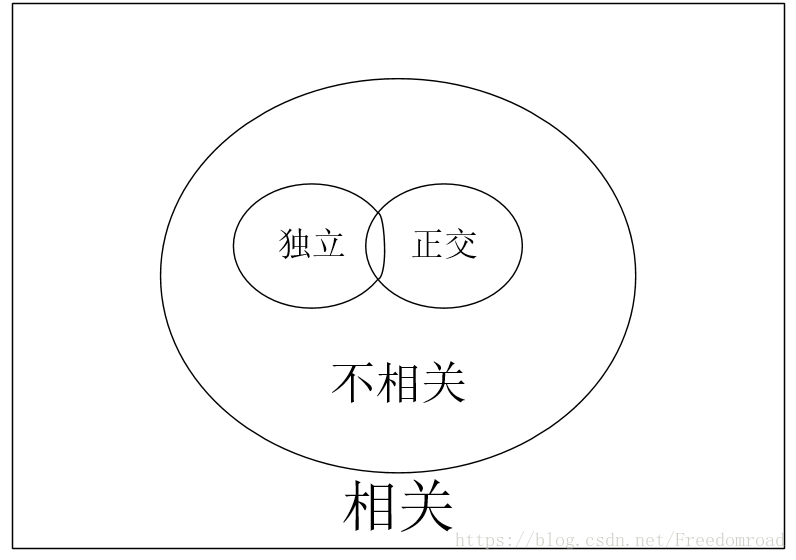
感觉这两个概念类似于平行四边形和菱形的关系,在初中学这两个几何概念时只要牢记判定定理和性质定理就可以解题

结论:

1.不相关一定独立,但是独立不一定不相关,即不相关条件更严格

2.目前课本上提到的均值,方差的性质都和不相关有关,当然从独立推到这些性质也是成立的

判定定理

独立性$F(x,y)=F_X(x)F_Y(y)$

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VulG7VUa-1646729696517)(https://gitee.com/deutschball/imperial-march/raw/master/X[G@0YEW2GO%U]QRO852GC8.jpg)]

A一定是错误的

B一定是正确的,任何随机变量都有分布律,也就都有分布函数

C只有对连续型随机变量成立,离散型随机变量没有概率密度这种东西

D不一定所有随机变量都有数学期望,比如柯西分布

设$X,Y$是两个随机变量,二者的联合分布函数$F(x,y)$,边缘分布函数分别为$F_X(x),F_Y(y)$,如果有
$$F(x,y)=F_X(x)F_Y(y)$$
则称随机变量$X,Y$相互独立

证明不独立只需要用P(AB)≠P(A)P(B)举反例

离散型

对于离散型随机变量X,Y,设其联合分布律为$P(X=x_i,Y=y_j)=p_{ij}$,边缘分布律为$P(X=x_i)=p_{i\cdot },P(Y=y_j)=p_{\cdot j}$

则X,Y相互独立的充要条件为
$$p_{ij}=p_{i\cdot }{p}_{\cdot j}$$

证明:

必要性证明

即证$F(x,y)=F_X(x)F_Y(y)\Rightarrow P(X=x,Y=y)=P(X=x)P(Y=y)$

这个证明是相对困难的,因为分布函数实际上是$P(X\le x,Y\le y)=P(X\le x)P(Y\le y)$的区间形式,而要证明的是点的形式

$P(X=x,Y=y)=P(X=x)P(Y=y)$

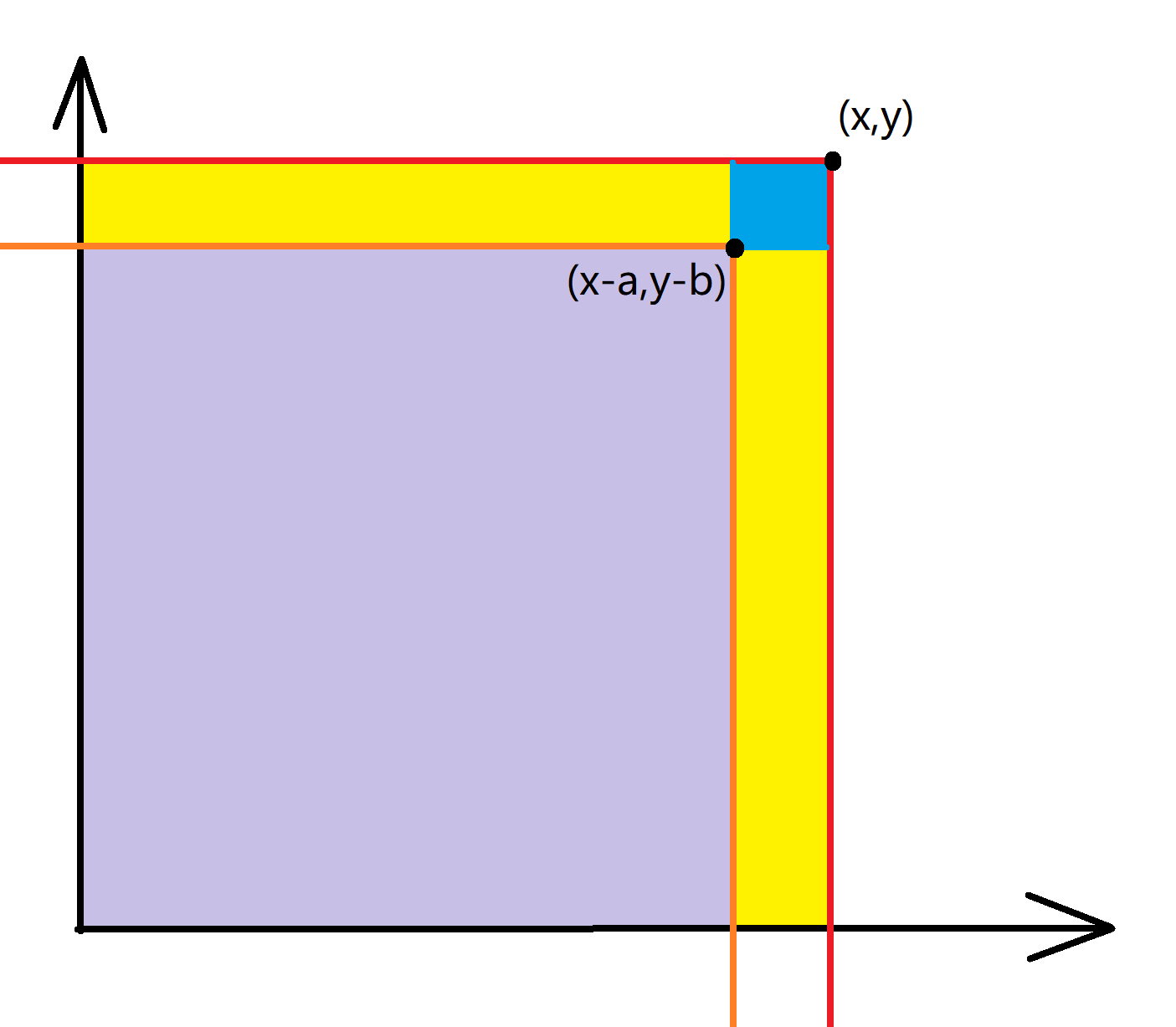
关键是如何从一个小于等于x小于等于y的区间降维到一个点(x,y)上.能够想到的是二维差分,

对联合分布律作二维差分得到
$$P(x-a\le X\le x,y-a\le Y\le y)=P(X\le x,Y\le y)+P(X\le x-a,Y\le y-b)-P(X\le x,Y\le y-b)-P(X\le x-a,Y\le y)$$

由已知条件$F(x,y)=F_X(x)F_Y(y)$得到:
$$P(X\le x,Y\le y)=P(X\le x)P(Y\le y)$$
那么有
P ( x − a ≤ X ≤ x , y − a ≤ Y ≤ y ) = P ( X ≤ x ) P ( Y ≤ y ) + P ( X ≤ x − a ) P ( Y ≤ y − b ) − P ( X ≤ x ) P ( Y ≤ y − b ) − P ( X ≤ x − a ) P ( Y ≤ y ) = P ( X ≤ x ) [ P ( Y ≤ y ) − P ( Y ≤ y − b ) ] + P ( X ≤ x − a ) [ P ( Y ≤ y ) − P ( Y ≤ y − b ) ] = [ P ( X ≤ x ) − P ( X ≤ x − a ) ] [ P ( Y ≤ y ) − P ( Y ≤ y − b ) ] = P ( x − a < X ≤ x ) P ( y − b < Y ≤ y ) \begin{aligned} &P(x-a\leq X\leq x,y-a\leq Y\leq y)\\ &=P(X\leq x)P(Y\leq y)+P(X\leq x-a)P(Y\leq y-b)-P(X\leq x)P(Y\leq y-b)-P(X\leq x-a)P(Y\leq y)\\ &=P(X\leq x)[P(Y\leq y)-P(Y\leq y-b)]+P(X\leq x-a)[P(Y\leq y)-P(Y\leq y-b)]\\ &=[P(X\leq x)-P(X\leq x-a)][P(Y\leq y)-P(Y\leq y-b)]\\ &=P(x-a< X\leq x)P(y-b< Y\leq y) \end{aligned} ​P(x−a≤X≤x,y−a≤Y≤y)=P(X≤x)P(Y≤y)+P(X≤x−a)P(Y≤y−b)−P(X≤x)P(Y≤y−b)−P(X≤x−a)P(Y≤y)=P(X≤x)[P(Y≤y)−P(Y≤y−b)]+P(X≤x−a)[P(Y≤y)−P(Y≤y−b)]=[P(X≤x)−P(X≤x−a)][P(Y≤y)−P(Y≤y−b)]=P(x−a<X≤x)P(y−b<Y≤y)​
对于给定的x,y有
$$
\lim_{a\rightarrow x,b\rightarrow y}P(x-a\leq X\leq x,y-a\leq Y\leq y)=P(X=x,Y=y)\

\lim_{a\rightarrow x,b\rightarrow y}=P(x-a< X\leq x)P(y-b< Y\leq y)=P(X=x)P(Y=y)\

P(X=x,Y=y)=P(X=x)P(Y=y)
$$
证毕

充分性证明

$P(X=x,Y=y)=P(X=x)P(Y=y)\Rightarrow F(x,y)=F_X(x)F_Y(y)$
$$\begin{array}{rl}& P(X\le x_i,Y\le y_i)\\ & =\sum _{k=1}^i\sum _{l=1}^{j}P(X=x_k,Y=y_l)\\ & =\sum _{k=1}^i\sum _{l=1}^{j}P(X=x_k)P(Y=y_l)\\ & =[\sum _{k=1}^{i}P(X=x_k)][\sum _{l=1}^{j}P(Y=y_l)]\\ & =P(X\le x_i)P(Y\le y_j)\end{array}$$
证毕

连续型

对于连续型随机变量X,Y,设其联合概率密度为$f(x,y)$,边缘概率密度分别为$f_X(x),f_Y(y)$,则$X,Y$相互独立的充要条件为:
$$f(x,y)=f_X(x)f_Y(y)$$

证明:

必要性证明

即证$F(x,y)=F_X(x)F_Y(y)\Rightarrow f(x,y)=f_X(x)f_Y(y)$
$$f(x,y)=\frac{{\partial }^{2}F(x,y)}{\partial x\partial y}=\frac{\partial F_X(x)}{\partial x}\frac{\partial F_Y(y)}{\partial y}=f_X(x)f_Y(y)$$
充分性证明

即证$f(x,y)=f_X(x)f_Y(y)\Rightarrow F(x,y)=F_X(x)F_Y(y)$
$$\begin{gathered} F(x,y)={\int }_{-\infty }^x{\int }_{-\infty }^{y}f(x,y)dxdy \\ ={\int }_{-\infty }^x{\int }_{-\infty }^y{f}_X(x)f_Y(y)dxdy \\ ={\int }_{-\infty }^x{f}_X(x)dx{\int }_{-\infty }^y{f}_Y(y)dy \\ =F_X(x)F_Y(y) \end{gathered}$$
证毕

不相关${\rho }_{xy}=0$(协方差为0)

设随机变量X,Y的相关系数为${\rho }_{xy}$,如果${\rho }_{xy}=0$则称随机变量X,Y线性无关,即不相关

相关系数其计算公式为
$${\rho }_{xy}=\frac{cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}$$
其中$cov(X,Y)$为随机变量X,Y的相关系数,其计算公式为
$$cov(X,Y)=E[(X-EX)(Y-EY)]=E(XY)-E(X)E(Y)$$

在证明随机变量不相关时一定用协方差等于0判断

性质定理

独立

当Y关于X的条件概率密度函数中没有出现x时,随机变量X和Y相互独立

出乎意料的一个结论,在做2019-2020概率论期末卷子时答案是这么写的

已知$X\sim U(2,3)$当$X=x$时$f_{Y|X}(y|x)=\{\begin{array}{l}1,1\le y\le 2\\ 0,其他\end{array}$

答案直接说"条件概率和x无关,因此X,Y相互独立",

???

不相关

充要条件$E(XY)=E(X)E(Y)$

由X,Y不相关得到${\rho }_{xy}=0$那么$cov(X,Y)=0$那么$E(XY)=E(X)E(Y)$,显然不相关和$E(XY)=E(X)E(Y)$互为充要条件

充要条件$a,b\ne 0,D(aX+bY)=0$

$$\begin{array}{rl}D(aX+bY)& =E(aX+bY{)}^2-E^2(aX+bY)\\ & =E(a^2{X}^2+2abXY+b^2{Y}^2)-(aE(X)+bE(Y){)}^2\\ & =2abE(XY)-2abE(X)E(Y)\\ & =2ab(E(XY)-E(X)E(Y))\\ & =0\end{array}$$

因而$E(XY)=E(X)E(Y)$

独立和不相关的关系

任何情况下独立$\Rightarrow$不相关

X,Y独立证明$E(XY)=E(X)E(Y)$

$$E(XY)={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }xyf(x,y)dxdy$$

又X,Y相互独立,由连续性随机变量的判定定理有$f(x,y)=f_X(x)f_Y(y)$带入上式得到
$$\begin{gathered} E(XY)={\int }_{-\infty }^{+\infty }x{f}_X(x)dx{\int }_{-\infty }^{+\infty }y{f}_Y(y)dy \\ =E(X)E(Y) \end{gathered}$$

不相关无法证明独立的例子

由X,Y不相关得到:
$${\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }xy[f(x,y)-f_X(x)f_Y(y)]dxdy$$
下面举例$f(x,y)-f_X(x)f_Y(y)\ne 0$但是上式仍然成立的例子

令$f(x,y)-f_X(x)f_Y(y)=\frac{1}{x}+\frac{1}{y}$,带入上式得到:
$$\begin{gathered} {\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }xy[f(x,y)-f_X(x)f_Y(y)]dxdy \\ ={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }(y+x)dxdy \end{gathered}$$
取一个对称的上下界a,
$$\begin{array}{rl}& {\int }_{-a}^{+a}{\int }_{-a}^{+a}(x+y)dxdy\\ & ={\int }_{-a}^{+a}dy[\frac{1}{2}{x}^2+yx{]}_{-a}^{+a}\\ & =a{\int }_{-a}^{+a}d{y}^2\\ & =0\end{array}$$
那么
$$\underset{a\to +\infty }{\lim }{\int }_{-a}^{+a}{\int }_{-a}^{+a}(x+y)dxdy=0$$

即此时X,Y不相关,但是不能得到X,Y相互独立

只有正态随机变量X,Y相互独立$\iff$X,Y不相关

证明:

即证当正太随机变量X,Y不相关时,必有$f(x,y)=f_X(x)f_Y(y)$

二维正正态分布联合概率密度为
$$f(x,y)=\frac{1}{2\pi {\sigma }_1{\sigma }_2\sqrt{1-{\rho }^2}}{e}^{-\frac{1}{2(1-{\rho }^2)}[\frac{(x-{\mu }_1{)}^2}{{\sigma }_1^2}-2\rho \frac{(x-{\mu }_1)(x-{\mu }_2)}{{\sigma }_1{\sigma }_2}+\frac{(x-{\mu }_2{)}^2}{{\sigma }_2^2}]}$$
至于这个式子怎么来的,我不知道
$$\begin{gathered} f_X(x)=\frac{1}{\sqrt{2\pi }{\sigma }_1}{e}^{-\frac{(x-{\mu }_1{)}^2}{2{\sigma }_1^2}} \\ {f}_Y(y)=\frac{1}{\sqrt{2\pi }{\sigma }_2}{e}^{-\frac{(x-{\mu }_2{)}^2}{2{\sigma }_2^2}} \end{gathered}$$
如果有$f(x,y)=f_X(x)f_Y(y)$则必有$\rho =0$

而$\rho ={\rho }_{xy}$为X,Y的相关系数,当X,Y不相关时显然相关系数为0

设(X,Y)服从二维正态分布,且有$D(X)={\sigma }_X^2,D(Y)={\sigma }_Y^2$,

证明:当$a=\frac{{\sigma }_x^2}{{\sigma }_Y^2}$,随机变量$W=X-aY$与随机变量$V=X+aY$相互独立

显然W,V是X,Y的线性组合,也服从于二维正态分布

由正态随机变量X,Y相互独立$\iff$X,Y不相关,我们只需要证明一个相对比较弱的命题:W,V不相关

即证$cov(W,V)=0$

$cov(W,V)=E(WV)-E(W)E(V)=E(X^2-a^2{Y}^2)-0=E(X^2)-a^{2}E(Y^2)$

而

$E(X^2)=D(X)+E^2(X)=D(X)={\sigma }_X^2$

$E(Y^2)=D(Y)+E^2(Y)=D(Y)={\sigma }_Y^2$

故$cov(W,V)=0$即W,V不相关

因而正态随机变量W,V独立

证明独立因此可以对于正态随机变量证明不相关