第3、7题难在了数学思路上(不会或理解不了私信)
仅代表个人看法
如有错误请指正
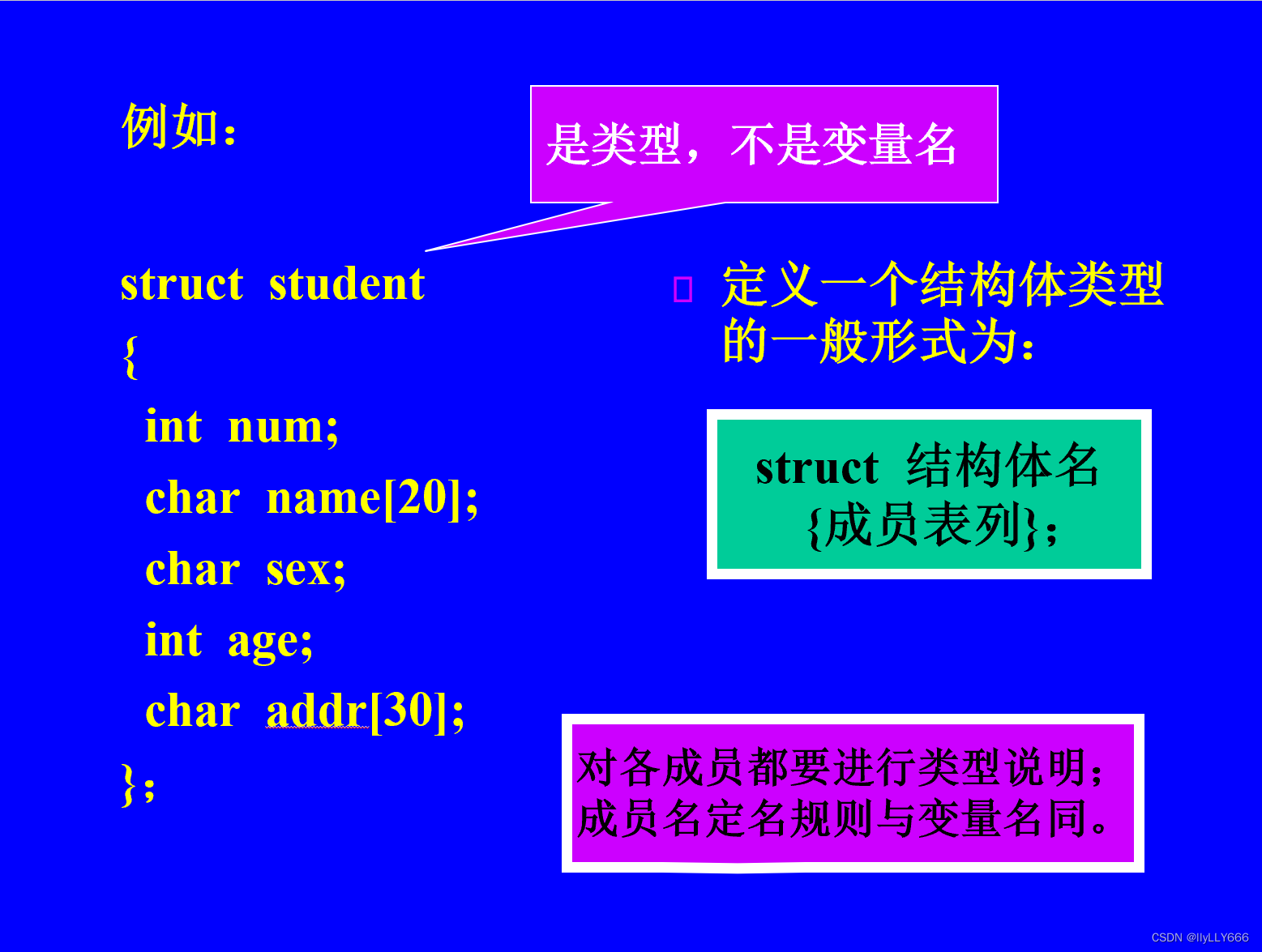
题目1:用筛选法求100 之内的素数。
代码如下:
#include <stdio.h>
#include <math.h>
int main()
{
int i, j, n, a[101];
for (i = 1; i <= 100; i++)
a[i] = i;
a[1] = 0;
for (i = 2; i < sqrt(100); i++)
for (j = i + 1; j <= 100; j++)
{
if (a[i] != 0 && a[j] != 0)
if (a[j] % a[i] == 0)
a[j] = 0;
}
printf("\n");
for (i = 2, n = 0; i <= 100; i++)
{
if (a[i] != 0)
{
printf("%5d", a[i]);
n++;
}
if (n == 10)
{
printf("\n");
n = 0;
}
}
printf("\n");
return 0;
}

数学思路讲解(可能讲的不好,多多包涵)
(1)先将1挖掉(因为1不是素数)。
(2)用2除它后面的各个数,把能被2整除的数挖掉,即把2的倍数挖掉。
(3)用3除它后面各数,把3 的倍数挖掉。
(4)分别用4,5…各数作为除数除这些数以后的各数。这个过程一直进行到在除数后面的数已全被挖掉为止。例如在图6.1中找1~50 的素数,要一直进行到除数为 47为止。事实上,可以简化,如果需要找1~n 的素数,只须进行到除数为 n(取其整数)即可,例如对1~50,只须进行到将 7 作为除数即可。
题目2:用选择法对10个整数排序。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int main()
{
int i, j, min, temp, a[11];
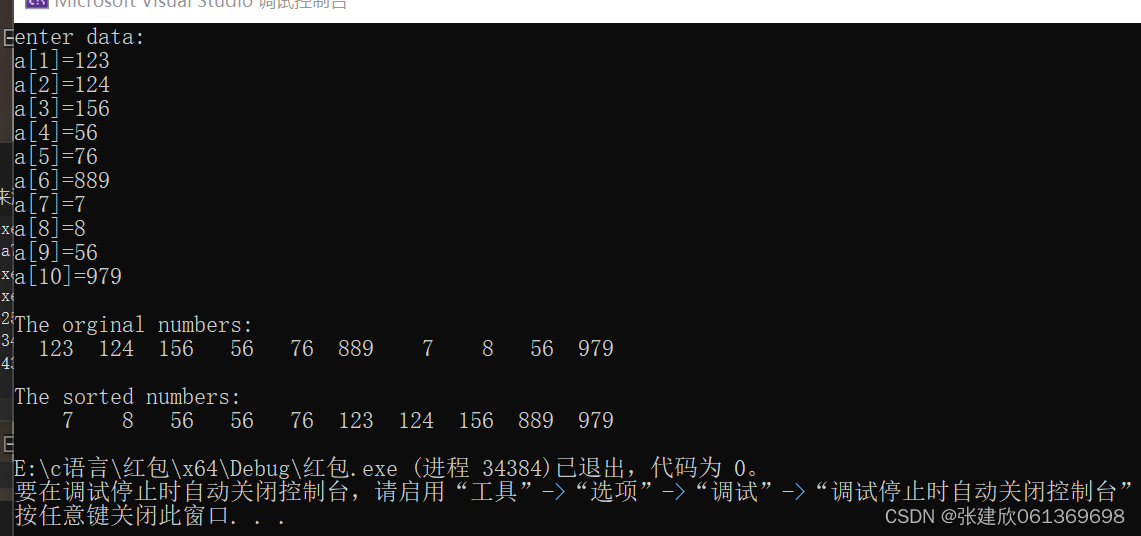
printf("enter data:\n");
for (i = 1; i <= 10; i++)
{
printf("a[%d]=", i);
scanf("%d", &a[i]);
}
printf("\n");
printf("The orginal numbers:\n");
for (i = 1; i <= 10; i++)
printf("%5d", a[i]);
printf("\n");
for (i = 1; i <= 9; i++)
{
min = i;
for (j = i + 1; j <= 10; j++)
if (a[min] > a[j])
min = j;
temp = a[i];
a[i] = a[min];
a[min] = temp;
}
printf("\nThe sorted numbers:\n");
for (i = 1; i <= 10; i++)
printf("%5d", a[i]);
printf("\n");
return 0;
}
数学思路:
设有10个元素 a[1]~a[10],将 a[1] 与 a[2]~a[10] 比较,若 a[1] 比 a[2]~a[10] 都小,则不进行交换,即无任何操作。若 a[2]~a[10] 中有一个以上比 a[1] 小,则将其中最大的一个(假设为 a[i] )与 a[1] 交换,此时 a[1] 中存放了10 个中最小的数。第 2 轮将 a[2] 与 a[3]~a[10] 比较,将剩下 9 个数中的最小者 a[i] 与 a[2] 对换,此时a[2] 中存放的是10 个中第二小的数。依此类推,共进行 9 轮比较,a[1]~a[10] 就已按由小到大的顺序存放了。
(如果还不会,请留言)
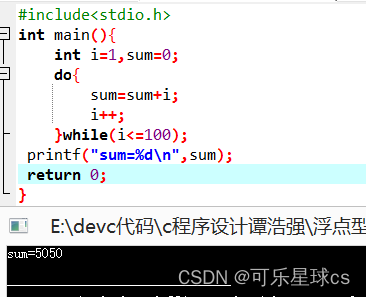
题目3:求一个 3×3 的整型矩阵对角线元素之和。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int main()
{
int a[3][3], sum = 0;
int i, j;
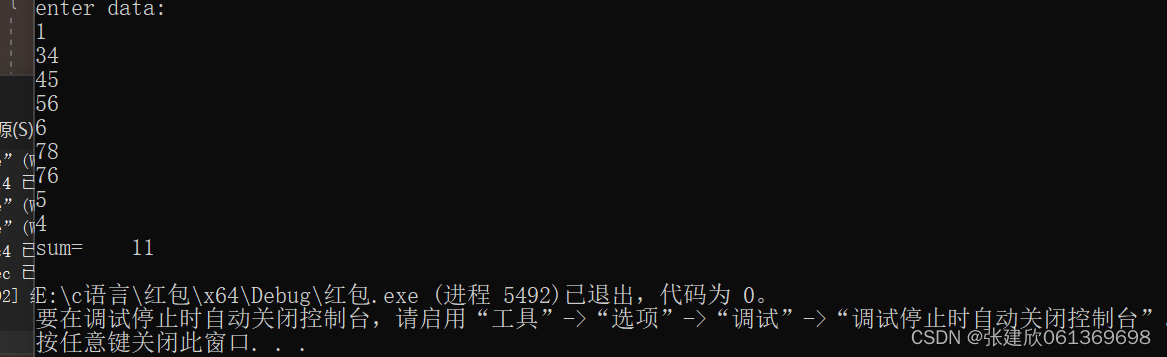
printf("enter data:\n");
for (i = 0; i < 3; i++)
for (j = 0; j < 3; j++)
scanf("%3d", &a[i][j]);
for (i = 0; i < 3; i++)
sum = sum + a[i][i];
printf("sum=%6d\n", sum);
return 0;
}
插几句题外话
我们都知道在程序的 scanf 语句中用"%d"作为输入格式控制,上面输入数据的方式显然是可行的。那么也可以在一行中连续输入9个数据,如:
1 2 4 5 24 56 59 28 23
发现输出结果也一样。在输入完9个数据并按回车键后,这 9个数据被送到内存中的输入缓冲区中,然后逐个送到各个数组元素中,所以输出结果都是一样的。
实验注意(程序中用的是整型数组,运行结果是正确的。如果用的是实型数组,只须将程序第4 行的 int 改为 float 或 double 即可,在输入数据时可输入单精度或双精度的数,程序也可以运行)
题目4:有一个已排好序的数组,要求输入一个数后,按原来排序的规律将它插入数组中。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int main()
{
int a[11] = { 1, 4, 6, 9, 13, 16, 19, 28, 40, 100 };
int temp1, temp2, number, end, i, j;
printf("array a:\n");
for (i = 0; i < 10; i++)
printf("%5d", a[i]);
printf("\n");
printf("insert data:");
scanf("%d", &number);
end = a[9];
if (number > end)
a[10] = number;
else
{
for (i = 0; i < 10; i++)
{
if (a[i] > number)
{
temp1 = a[i];
a[i] = number;
for (j = i + 1; j < 11; j++)
{
temp2 = a[j];
a[j] = temp1;
temp1 = temp2;
}
break;
}
}
}
printf("Now aray a:\n");
for (i = 0; i < 11; i++)
printf("%5d", a[i]);
printf("\n");
return 0;
}

题目5:将一个数组中的值按逆序重新存放。例如,原来顺序为8,6,5,4,1。要求改为1,4,5,6,8。
答案代码
# <stdio.h>
#define N 5
int main()
{
int a[N], i, temp;
printf("enter includearray a:\n");
for (i = 0; i < N; i++)
scanf("%d", &a[i]);
printf("array a:\n");
for (i = 0; i < N; i++)
printf("%4d", a[i]);
for (i = 0; i < N / 2; i++)
{
temp = a[i];
a[i] = a[N - i - 1];
a[N - i - 1] = temp;
}
printf("\nNow,array a:\n");
for (i = 0; i < N; i++)
printf("%4d", a[i]);
printf("\n");
return 0;
}
结果

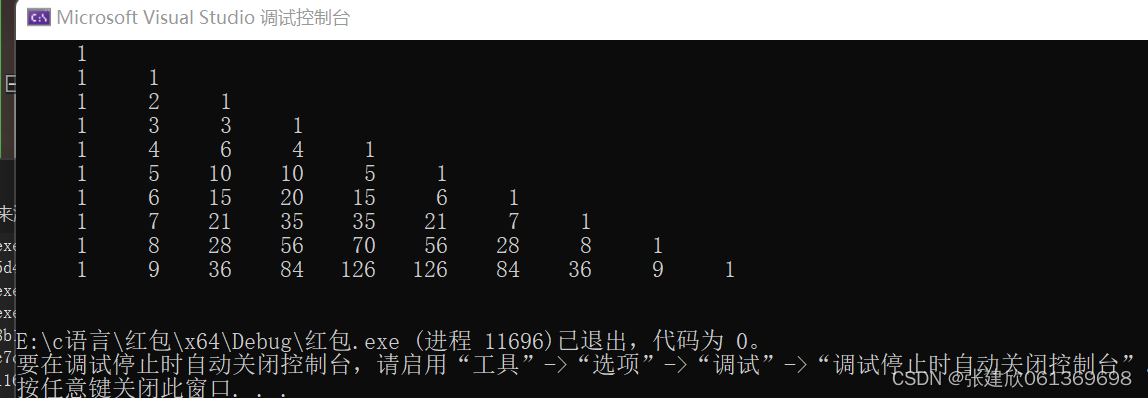
题目6:输出以下的杨辉三角形(要求输出 10行)
#include <stdio.h>
#define N 10
int main()
{
int i, j, a[N][N];
for (i = 0; i < N; i++)
{
a[i][i] = 1;
a[i][0] = 1;
}
for (i = 2; i < N; i++)
for (j = 1; j <= i - 1; j++)
a[i][j] = a[i - 1][j - 1] + a[i - 1][j];
for (i = 0; i < N; i++)
{
for (j = 0; j <= i; j++)
printf("%6d", a[i][j]);
printf("\n");
}
printf("\n");
return 0;
}
题目7:输出"魔方阵"。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int main()
{
int a[15][15], i, j, k, p, n;
p = 1;
while (p == 1)
{
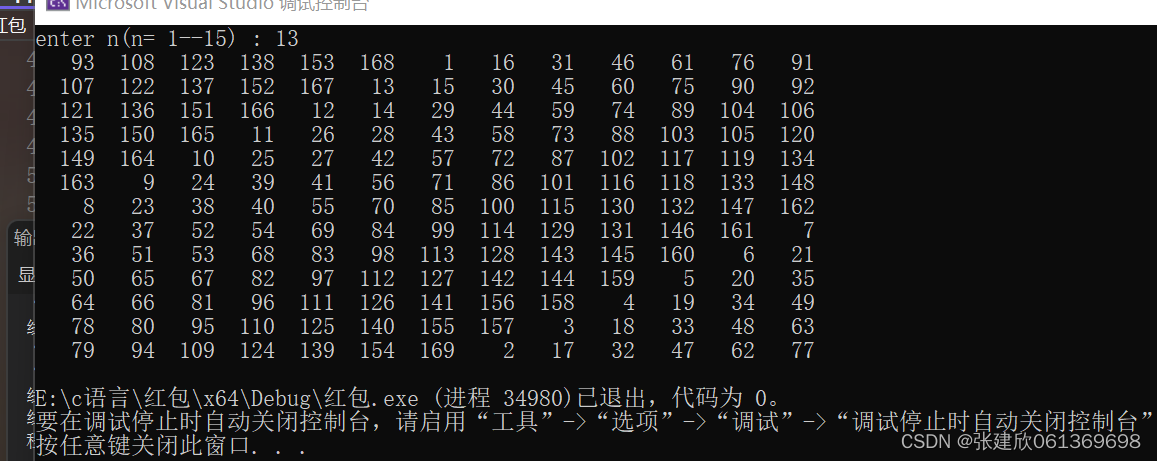
printf("enter n(n= 1--15) : ");
scanf("%d", &n);
if ((n != 0) && (n <= 15) && (n % 2 != 0))
p = 0;
}
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
a[i][j] = 0;
j = n / 2 + 1;
a[1][j] = 1;
for (k = 2; k <= n * n; k++)
{
i = i - 1;
j = j + 1;
if ((i < 1) && (j > n))
{
i = i + 2;
j = j - 1;
}
else
{
if (i < 1)
i = n;
if (j > n)
j = 1;
}
if (a[i][j] == 0)
a[i][j] = k;
else
{
i = i + 2;
j = j - 1;
a[i][j] = k;
}
}
for (i = 1; i <= n; i++)
{
for (j = 1; j <= n; j++)
printf("%5d", a[i][j]);
printf("\n");
}
return 0;
}
结果如下
该题想法
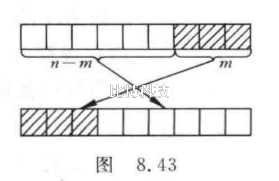
(1)将 1 放在第 1 行中间一列。
(2)从 2 开始直到 n×n 止,各数依次按此规则存放:每一个数存放的行比前一个数的行数减 1 ,列数加 1。
(3)如果上一数的行数为 1,则下一个数的行数为 n(指最下一行)。例如,1 在第 1 行,则 2 应放在最下一行,列数同样加 1。
(4)当上一个数的列数为 n 时,下一个数的列数应为 1,行数减 1。例如,2 在第 3 行最后一列,则 3 应放在第 2 行第 1 列。
(5)那么按上面规则确定的位置上已有数,或上一个数是第 1 行第 n 列时,则把下一个数放在上一个数的下面。例如,按上面的规定,4 应该放在第 1 行第 2 列,但该位置已被 1 占据,所以 4 就放在 3 的下面。由于 6 是第 1 行第 3 列(即最后一列),故 7 放在 6 下面。
本文遵守 Creative Commons 协议
如有征用请说明
谢谢点赞与浏览