1129 -- Channel Allocation (poj.org)

题意：

大致的题意就是给你一张图，给这张图染色，最多能染多少种颜色

思路：

首先要构造状态图，构造完状态图之后对其进行搜索（注意是先有图再有的dfs，而不是边dfs边构图，这个是观念的变化）

我们考虑一个状态图的顶点为一个染色方案

类似于这样，这是状态图的一个顶点

  

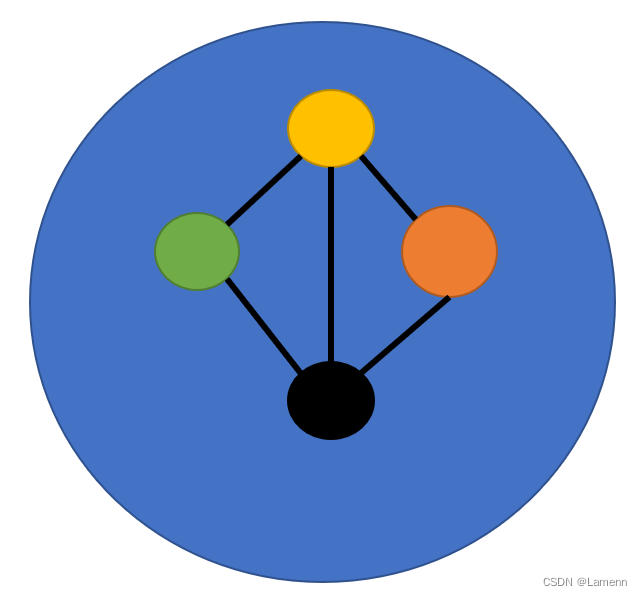
 一开始的顶点里面的图是一个都没染色的，然后从起点开始转移出去26条边，深度为1的点里面的图是一个点染成26种颜色的情况

这样我们脑子里的图就构造好了，我们去在这个状态图里面dfs，dfs的深度就是顶点里的图已经被染色的点的个数，所以出口就是dep>n

然后对于状态图的一个顶点，我们去枚举状态图的顶点中的图的其中一个顶点的颜色，并用数组标记（注意在状态图里的顶点可能是乱序遍历到的，即有可能是东染一个，西染一个，这个由题目给出的图本身决定

枚举颜色后，我们去check这个颜色是否合法，那只需要遍历这个点相邻的点，看有没有相邻点的颜色相同，若存在颜色相同的点就不合法

我的写法就是用链式前向星存题目里给出的图

Code：

#include <stdio.h>
#define max(a,b) (a>b?a:b)
using namespace std;
const int mxn=30,mxe=1e3+10;
int n,tot=0,ans=-1;
int head[mxn],c[mxn];
struct ty{int to,next;
}edge[mxe<<1];
void add(int u,int v){edge[tot].to=v;edge[tot].next=head[u];head[u]=tot++;
}
void init(){tot=0;ans=-1;for(int i=0;i<=n;i++){head[i]=-1;c[i]=0;}
}
bool check(int u){for(int i=head[u];~i;i=edge[i].next){if(c[edge[i].to]==c[u]) return false;}return true;
}
bool dfs(int dep){if(dep>n) return true;for(int i=1;i<=26;i++){c[dep]=i;if(check(dep)){if(dfs(dep+1)) return true;}c[dep]=0;}return false;
}
int main(){while(scanf("%d",&n)==1&&n){init();getchar();for(int i=1;i<=n;i++){getchar();getchar();char ch;while(ch=getchar()){if(ch=='\n') break;add(i,ch-'A'+1);}}dfs(1);for(int i=1;i<=n;i++) ans=max(ans,c[i]);if(ans==1) printf("%d channel needed.\n",ans);else printf("%d channels needed.\n",ans);}return 0;
}

总结：

1.在搜索之前，先想好我们需要构造的状态图，想好状态图之后再去写代码会好想很多

2.一个方案作为一个状态图的顶点很常见