李嘉图模型

单一要素经济模型

相对价格与供给

产品$i$生产者的工资率为$\frac{P_i}{{\alpha }_i}$，工人们倾向生产工资率更高的商品。
在国际贸易中，考虑两国的劳动生产率${\alpha }_i/{\alpha }_i^{\ast }$，本国会优先生产劳动生产率相对较高的那个产品，即该产品具有比较优势。
相对价格的确定使用一般均衡分析：

贸易所得

从消费可能性边界考虑

相对工资

#TODO

多种、连续产品的拓展

其他概念

• 运输费用：冰山成本，运输产品所需的运输费用，以及运输过程中的产品损耗
• 非贸易品：各国自给自足的产品

专用要素模型

孤立经济的情况

设存在3种要素$L,K,T$，以及两种产品$F,M$。
其生产函数为：$Q_F=Q_F(L_F,K),Q_M=Q_M(L_M,T)$，
劳动要素投入量$L=L_F+L_M$
边际产品价格等于要素价格，即：
$$\begin{gathered} p_M\frac{\partial Q_M}{\partial L_M}=p_F\frac{\partial Q_F}{\partial L_F}={\omega }_L \\ {p}_M\frac{\partial Q_M}{\partial K}={\omega }_K \\ {p}_F\frac{\partial Q_F}{\partial T}={\omega }_T \end{gathered}$$
由此可得到均衡产量组合

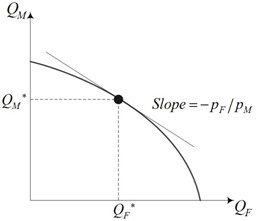
也就是说，相对产量由相对价格决定。

在国际贸易中

改变的是相对供给曲线$RS$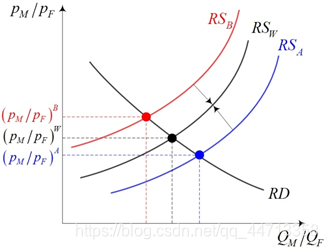
这一改变也可以理解为一国要素禀赋发生变化时产生的影响。给定其他条件不变：
(1) 如果一国资本禀赋增加，则其M-F相对供给曲线向右下方移动，该国经济实现孤立均衡时的M-F相对价格下降，M部门使用的劳动数量增加，F部门使用的劳动数量减少；
(2) 如果一国土地禀赋增加，则其M-F相对供给曲线向左上方移动，该国经济实现孤立均衡时的M-F相对价格上升，M部门使用的劳动数量减少，F部门使用的劳动数量增加；
(3) 如果一国劳动禀赋增加，则M和F的产量都增加，对于产品相对产量的影响不确定。

贸易模式

显然，一国将出口其在孤立经济条件下相对价格较低的产品。根据前面的分析，如果两国只在(专用)要素禀赋上存在差异，那么拥有相对充裕的某种要素禀赋的国家，在孤立均衡条件下其使用该种要素的生产部门的产品将在开放国际贸易时成为该国的出口产品。

影响

• 本国出口部门使用的专门要素获益；
• 本国进口部门使用的专门要素受损；
• 移动要素受到的影响不确定。

Heckscher-Ohlin模型

要素禀赋——比较优势

要点

• 222（要素，产品，国家）
• 生产技术相同（Ricado模型假设生产技术不同）
• 要素禀赋（相对丰裕程度）不同
• 生产两种产品有着不同的要素相对密集程度
• 古典性所有产品的生产技术都是规模报酬不变的，所有产品和要素市场都是完全竞争的

表述

• 资本，劳动使用量$k,l$，其对应的禀赋为$K,L$

中略

新贸易理论

放松的假设：

• 不完全竞争市场
• 规模报酬递增

垄断竞争模型(1979)

• 产品差异化
• 偏好多样性

CES效用函数

(就记成$x$的$L^{\rho }-norm$也就是$||x|{|}_{\rho }$)
$$U=[{\int }_{\omega \in \Omega }{x}^{\rho }(\omega )d\omega {]}^{\frac{1}{\rho }}$$
替代弹性$\sigma =\frac{1}{1-\rho }$
需要注意的是，这里只讨论一个产业，也就是说，不同的产品种类只表示不同的产品品牌

• 我们用EMP（支出最小化）刻画消费者的行为，得到：（这里就是变分法）
  $$\frac{x({\omega }_1)}{x({\omega }_2)}=[\frac{p({\omega }_1)}{p({\omega }_2)}{]}^{\frac{1}{\rho -1}}$$
• 也就是说，我们可以用一种商品的消费$x({\omega }_0)\equiv x_0$来表示其他商品的消费：(应当注意到$x_0$是常数)
  $$\begin{array}{rl}\bar{u}& =x_0{p}_0[\int p^{-\frac{\rho }{1-\rho }}d\omega {]}^{\frac{1}{\rho }}\\ & \equiv x_0{p}_0^{\sigma }{P}^{-\sigma }\end{array}$$
  $P$可以认为是（加权的）价格指数：
  $$P\equiv ||p(\omega )|{|}_{1-\sigma }$$
• 由于${\omega }_0$是任意的，因此我们用$\omega$替代它，就得到了任意产品的Hicks需求函数：
  $$x(\omega )=\bar{u}{p}^{-\sigma }(\omega )P^{\sigma }$$
  该产品的支出：
  $$e(\omega )=px=\bar{u}{p}^{1-\sigma }{P}^{\sigma }$$
  总支出：
  $$E=\int ed\omega =\bar{u}P$$
• 也就是说，消费者的行为等价于用一个总体价格购买一个总体商品
• 由此，我们可以得到已知支出&价格（而非效用&价格）的Mashell需求函数
  $$x(\omega )=\frac{I}{P}{p}^{-\sigma }(\omega )P^{\sigma }=I{p}^{-\sigma }(\omega )P^{\sigma -1}$$

规模报酬递增

一种最简单的刻画：

$f$	固定成本
$w$	工资率
$L$	劳动（唯一的生产要素）
$\phi$	劳动的边际产出（const）

于是，生产$q$单位产品的成本：
$$c(q)=w[f+\frac{q}{\phi }]$$
于是，边际成本$MC=w/\phi$
平均成本：$AC=w({\phi }^{-1}+f{q}^{-1})$

由于不考所以只写重要结论和推导思路

经济均衡

• 孤立经济均衡
  • （利润最大化）厂商的定价行为
    $$p(\omega )=\frac{\text{w}}{\rho \phi }$$
  • 即所有产品的价格是相同的。也就是说产品价格是其单位成本的一个不变加成（不变加成定价法则）
  • 将该定价带入其他式中
    $$P=||\frac{\text{w}}{\rho \phi }|{|}_{1-\sigma }=\frac{\text{w}}{\rho \phi }{\mu }^{\frac{1}{1-\sigma }}(\Omega )\equiv \frac{\text{w}}{\rho \phi }{M}^{\frac{1}{1-\sigma }}$$
    $$q(\omega )=R\rho \phi M^{-1}$$
  • 再带入利润函数得到
    $$\pi (\omega )=(1-\rho )R{M}^{-1}-f$$
    (要注意$R=\text{w}L$)
  • 由零利润条件得到商品种类数量（其测度）应满足：
    $$\begin{gathered} L{M}^{-1}-f-L\rho M^{-1}=0 \\ M=\frac{(1-\rho )L}{f} \end{gathered}$$
  • 最终得到：
    1. $$P=(\rho \phi {)}^{-1}{f}^{\frac{1}{\sigma -1}}{L}^{\frac{1}{1-\sigma }}(1-\rho {)}^{\frac{1}{1-\sigma }}$$
    2. $$q=\frac{\rho \phi f}{1-\rho }$$
    3. $$x=q/L=\frac{\rho \phi f}{(1-\rho )L}$$
    4. $$u=P^{-1}$$
  • 于是效用和经济规模$L$正相关
• 自由贸易均衡
  • 各国所有产品价格相等（记为$p^{\ast }$）
  • 因此，工资率必然相等，即$p^{\ast }=\frac{\text{w}}{\rho \phi }$
  • 注意到此时劳动禀赋与商品种类等于两国之和
  • 其他推导同孤立均衡
• 结论：
  • 两种均衡下的产品均衡数量没有发生变化
  • 但每个消费者消费的数量，实际更少了
  • 贸易的理由：
    • 厂商的市场空间增大，从而得以火大生产规模，获得规模报酬递增的收益。
    • 消费者福利都得到了改进（原因：生产效率提高，收入提高。购买的产品种类而非每种产品的数量增加。）

引力方程

计算产业内（即$\Omega$）贸易的规模

• 产自本国($H$)的产品，$L^H/(L^H+L^F)$的部分在本国销售，其余出口。
• 本国生产的产品种类
  • 两国不太可能同时生产一种商品（因为要分别支付固定成本）
  • 有生产技术解得投入到每种产品的劳动量$l^{\ast }=\frac{f}{1-\rho }$
  • $$M^C=\frac{(1-\rho )L^C}{f}$$
  • 容易得到贸易自然平衡，贸易额$V=\frac{L^H{L}^F}{L^H+L^F}$

Krugman模型的总结

• 古典贸易理论只考虑产业间贸易
• 暗示了国家间的要素禀赋差异不是那么的重要，或者已经被国际贸易挖掘殆尽，从而新的国际贸易增长主要来自于产业内

母国市场效应(1980)

贸易模式的决定——出口何种商品

两类消费者——两类产品

国内存在两类消费者（$\alpha ,\beta$），分别偏好产业内的$\alpha$和$\beta$
类产品。
这两类消费者的效用形式同Krugman的基本模型。也即：

• 某类消费者的效用和该类型产品的生产规模$L_t$正相关
• 各种类产品的均衡产量和均衡价格均相同。
• 某类消费者的效用更高是因为他们消费了更多种类的产品（事实上每种产品的均衡消费量更低了）

贸易模式的确定

考虑两个国家的消费者数量不同，具体而言：
$$\begin{gathered} L_{\alpha }^H>L_{\alpha }^F \\ {L}_{\beta }^H<L_{\beta }^F \end{gathered}$$
显然，贸易均衡下，各国两类产品的生产种类是未定的。

这是因为两国消费者的偏好差异对于两国生产者而言没有区别性 —— 任何一国的生产者都是同等地面对本国的某类消费者和外国的某类消费者。

为了决定贸易模式，需要引入冰山成本

• 设损失率为$1-\delta$
• 则本国生产的产品供应本国市场的单位成本为$w$，供应外国市场的单位成本为$w/\delta$
• 于是某国$C$市场上的$t$类型产品价格指数应当在集合${\Omega }_t^H\cup {\Omega }_t^F={\bigcup }_C{\Omega }_t$上求，测度$M_t=\mu ({\Omega }_t^H\cup {\Omega }_t^F)$
• 显然（但显然）${\Omega }_t^H\cap {\Omega }_t^F=\varnothing$即$M_t=M_t^H+M_t^F$

由此，某个厂商在两个市场上的利润最大化问题是彼此独立的。但等价于全球利润最大化的定价法则

• 于是，在某国$C$生产类型$t$产品的产商${\omega }_t^C$之定价法则为：
  $$p^C({\omega }_t^C)=\frac{{\text{w}}^C}{\rho \phi },p^{/C}({\omega }_t^C)=\frac{{\text{w}}^C}{\delta \rho \phi }$$
• 即出口的那部分定价会更高
• 结合${\Omega }_t^H\cap {\Omega }_t^F=\varnothing$，即可求出总体价格指数

一个显然的结论是：在考虑贸易成本的贸易均衡中，一国的经济规模（$L_{\alpha }^C+L_{\beta }^C$）越大，其在贸易均衡条件下的工资率就越高

但单独考虑某类型消费者的均衡支出（必定等于其收入$\omega$），可以得到：($\mathbf{R}$为两实数的序关系)
$$\begin{gathered} {\omega }^H\mathbf{R}{\omega }^F⟺M_{\alpha }^H\mathbf{R}{M}_{\alpha }^F \\ {\omega }^H\mathbf{R}{\omega }^F⟺M_{\beta }^H\mathbf{R}{M}_{\beta }^F \end{gathered}$$

在两国经济规模相等的情况下，上述两等价关系是矛盾的。从经济上看：零利润条件无法按在两国同时成立。

贸易均衡

• 我们只考虑两国完全对称的清露_{草，我为海盗船感到爽哥}(经济规模相等，一国的$\alpha$消费者等于另一国的$\beta$消费者）

• 显然，贸易均衡时，两国工资率相同

• 此时，通过分析价格指数$P_t^C$，均衡产量$q({\omega }_t^C)$，毛利润（销售额-可变成本），可以得到$\pi ({\omega }_t^C)$，某类厂商的利润之差${\pi }_t^C-{\pi }_t^{/C}$可以得到。
  $${\pi }_t^H-{\pi }_t^F=\left(\frac{L_t^H}{M_t^H+{\delta }^{\sigma -1}{M}_t^F}-\frac{L_t^F}{{\delta }^{\sigma -1}{M}_t^H+M_t^F}\right)(1-{\delta }^{\sigma -1})(1-\rho )$$

• 只要在均衡时两国都生产类型$t$的产品，那么应当有${\pi }_t^C={\pi }_t^{/C}=0$

• 容易得到：$$\begin{gathered} L_{\alpha }^H/L_{\alpha }^F=L_{\beta }^F/L_{\beta }^H\equiv \gamma \\ {M}_{\alpha }^C/M_{\alpha }^{/C}=M_{\beta }^{/C}/M_{\beta }^C=\frac{{\delta }^{\sigma -1}\gamma }{{\delta }^{\sigma -1}\gamma -1} \end{gathered}$$

• 也就是说{两国都生产两种产品}$⟺$$\gamma <{\delta }^{1-\sigma }$

• 当$\gamma$（两国的“品味差别”）不大时，才会出现上述状况，否则，两国将在两类别商品中专业化生产。

• 最后，通过零利润条件，可以得到均衡结果的闭解。

母国市场效应

开放贸易条件下，一国出口其拥有相对较大国内市场的产品，进口其拥有相对较小国内市场的产品

• 该效应依赖于贸易成本
• 本国市场较大，说明该类型产品在本国的生产规模较大，那么其边际成本较小，相较于外国的同类型产品有优势。

产业内与产业间贸易的同时分析(1981)

2*2*2的模型

• 两个国家 C ∈ { H , F } C\in\{H,F\} C∈{H,F}
• 两个产业 i ∈ I = { 1 , 2 } i\in I=\{1,2\} i∈I={1,2}
• 两种专用要素$L_i$只用于对应产业的生产

消费者行为——CES偏好

$$U^C=\prod _I{\left[{\int }_{{\Omega }_i}[x^C({\omega }_i){]}^{\rho }d{\omega }_i\right]}^{\frac{1}{\rho }}$$
在刻画消费者行为时，显然有$u_1{P}_1=u_2{P}_2$

生产者行为

• 这两类要素的价格（或者说工资）不必是一致的。
• 但是同样有产业内商品价格相同
• 再由零利润条件可以得到$M_1=M_2$
• 显然两产业产值相等，故有$w_1/w_2=L_2/L_1$

自由贸易均衡

• 假设两国经济结构对称（$L_1^H=L_2^F,L_1^F=L_2^H$）
• 可以证明分别位于两个国家的任意两家厂商生产的相同产业产品价格相同
• 由孤立均衡的各项条件可以退出，两个产业总产值相等。（又因为经济规模相同）因此有$w_1=w_2=w$
• 于是各产业内的价格指数同单一产业内的情况
• 最后由零利润条件可以得到内生均衡结果。

贸易模式

• 各国生产的产品种类满足：
  $$M_i^C=\frac{(1-\rho )L_i^C}{f}$$
• 因此，两国的产业间贸易量，等于每个产业间产品贸易量，即$$\begin{gathered} NE{X}_i^C=NI{M}_{/i}^C=NI{M}_i^{/C} \\ NE{X}_i^C=NE{X}_{/i}^{/C} \end{gathered}$$
• 注意此时产业内贸易模式仍是任意的（可以用母市场效应来确定）

新贸易理论与Heckerscher-Ohlin模型的结合(1981)

模型假设

• 同时存在产品同质的完全竞争产业与产品异质的垄断产业
• 是一个C*J*I（C个国家，J个产业，I种生产要素）模型

要素流动与聚集(1991)——“新经济地理”

均衡结论

• 有两种可能的均衡（主要与贸易成本有关）
• 在可移动要素更加集中的地区，该种要素获得的真实报酬始终高于其他地区，于是该种要素不断集中直至完全聚集到该地区（即产业聚集效应）
  • 导致聚集的离心力作用：
  • 母国市场效应
  • 价格指数效应
• 在可移动要素更加集中的地区，该种要素获得的真实报酬低于其他地区，于是要素的自由流动倾向于达到平衡分布（即地区收敛效应）
  • 导致收敛的平衡力作用：
  • 竞争程度效应

国际寡头模型

rua

政策含义（Krugman的教材上不少）

略

猩猩贸易理论

• 厂商异质性
• 厂商选择效应：出口部门只有一部分厂商是出口商
• 烤房毛衣会使落后的厂商退出市场，使其拥有的市场和要素流向先进厂商

Melitz模型(2003)

Melitz(2003)=Krugman(1979)+厂商异质性

outline

• 该模型是随机的。
• 厂商的固定成本$f$相同，但生产技术（生产效率）不同，即$\phi =\mathbb{C}(\Omega ,{\mathbb{R}}^{+})$，不妨以$\phi$代指厂商
• 厂商进入产业需要支付固定的进入成本$f_e$以获得生产技术，随后其生产技术$\phi$是随机的，服从分布$G$
• 产商的退出是随机的（以概率$\delta$）
• 经济的价格指数(需注意$\Phi ⫋\mathbb{R}$)$$P={\left[\frac{{\int }_{\Phi }{p}^{1-\sigma }(\phi )d\mu }{\mu (\Phi )}\right]}^{\frac{1}{1-\sigma }}$$
• _{(通过类似Krugman(1979)的分析)}可以得到厂商的产量与利润与$\phi$相关，那么就显然有一个临界技术水平${\phi }^{\ast }$，只有技术优于此的厂商才能在市场中获益，于是，市场中的产商$\Phi =({\phi }^{\ast },+\infty ]$
• 那么就能计算$\phi$的事后分布$G^{\prime }$(也可以对应成新的测度${\mu }^{\prime }$）
• 同时还有$\mu (\Phi )=1-G({\phi }^{\ast })$
• 虽然很有意思但是没时间复习了，算你m呢
• 于是价格指数可表示为
  $${\left[{\int }_{\Phi }{p}^{1-\sigma }(\phi )d{\mu }^{\prime }\right]}^{\frac{1}{1-\sigma }}$$
  有定价加成有$p=(\rho \phi {)}^{-1}$
  $$\begin{gathered} {\left[{\int }_{\Phi }(\rho \phi {)}^{\sigma -1}d{\mu }^{\prime }\right]}^{\frac{1}{1-\sigma }} \\ \equiv (\rho \psi {)}^{\frac{1}{1-\sigma }} \end{gathered}$$
  其中$\psi$相当于行业的加权平均生产率_{加权是因为其实质上相当于$\varphi$的$\sigma-1$阶矩}或行业总体生产V领
• ZCP与FE条件确定了${\phi }^{\ast }$

厂商间贸易——Antràs(2003)

厂商结构选择——Antràs,Helpman(2004)

厂商的投资和出口选择——HMY(2004)

基于异质性厂商的比较优势——BRS(2007)

异质性厂商的贸易政策——D&R-C(2009)

国际Bertrand竞争——BEJK(2003)

线性需求，内生成本——Melitz-Ottaviano(2008)