浮点数概述

浮点数，是属于有理数中某特定子集的数的数字表示，在计算机中用以近似表示任意某个实数。具体的说，这个实数由一个整数或定点数（即尾数）乘以某个基数（计算机中通常是2）的整数次幂得到，这种表示方法类似于基数为10的科学计数法。（该词条来源于百度百科）

N=(-1^S)×M×R^E
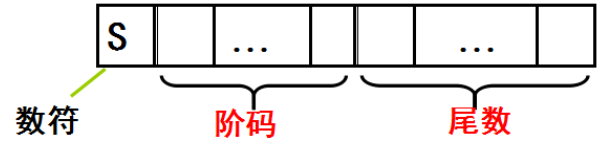
数符：浮点数的符号，0表示正数，1表示负数。
阶码：浮点数的指数，用移码表示，基数一般默认为2。阶码决定浮点数的取值范围。
尾数：“尾数”又可称之为“精度”，即对表达结果精确程度产生重要影响的数，也就是常说的significant digits，缩写后为significand（有效数，尾数）。尾数决定浮点数的精度，为了能够充分利用尾数表示更多的有效数字，通常叫尾数的绝对值限定在[0.5,1]，尾数用原码表示，因此要求原码的小数点的右边正数为1，负数为0。

浮点数的格式

浮点数有四种格式：单精度浮点数，双精度浮点数，扩充的单精度浮点数，扩充的多精度浮点数。

IEEE 754标准规定的浮点数的格式

在这里插入图片描述

IEEE 754偏移量与指数范围问题

问题描述：n位移码的表示范围明明是[-2^n-1 , 2^n-1-1]，偏移量是2^n-1，浮点数的指数使用移码表示，为什么n位浮点数的指数范围是[-2^n-1+ 2 , 2^n-1-1]，偏移量是2^n-1-1呢？即指数范围少了两个数，偏移量也少了一位。

移码的作用主要是方便浮点数的运算。阶码对阶需要比较两个浮点数阶码的大小，而阶码在补码的基础上偏移了+2^n-1，这样即使对于正负不相同的机器数，根据机器数实际的二进制数值也能轻松判断其大小。

对于IEEE 754中的单精度浮点数而言，其指数是8位，若偏移量是+2⁷（+128），则其真值的范围是[-128,127]，由于要使用阶码全0和全1来表示非规格化的值和特殊值，因此真值的范围变为[-127,126]，对应的浮点数范围变为：
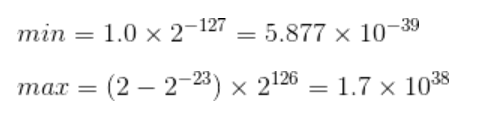
在这里插入图片描述
可以看出浮点数的表示范围左右很不对称，差的不止一丁半点，而是38个数量级。

若使用偏移量+127，除去非规格化值和特殊值后，其真值的范围变为[-126,127]，对应的浮点数范围变为：
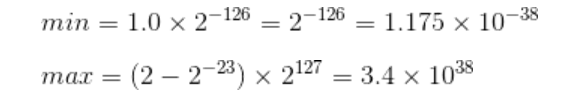
在这里插入图片描述
可以看到浮点数的表示范围很明显平衡了许多。

所以IEEE 754标准的移码较原有的移码，其指数范围少了两个数，偏移量也少了一位。移码顾名思义是一种对补码有偏移量的编码，无论偏移量是多少，都可以称之为移码，但是得更好地更合适地为我们所用。使用下面的四位补码和四位移码与它们的真值的对应关系中可以很直观地表述上述推理。

这是4位的补码与真值的对应关系

补码	真值
1000	-8
1001	-7
1010	-6
1011	-5
1100	-4
1101	-3
1110	-2
1111	-1
0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7

这是原来规定偏移量为8的4位的移码与真值的对应关系

移码	真值
0000	-8
0001	-7
0010	-6
0011	-5
0100	-4
0101	-3
0110	-2
0111	-1
1000	0
1001	1
1010	2
1011	3
1100	4
1101	5
1110	6
1111	7

这是为了防止浮点数范围不平衡新规定的偏移量为7的移码及其真值。

移码	真值
0000	非规格化值
0001	-6
0010	-5
0011	-4
0100	-3
0101	-2
0110	-1
0111	-0
1000	1
1001	2
1010	3
1011	4
1100	5
1101	6
1110	7
1111	特殊值

IEEE 754中浮点数值的三种情况：

1. 规格化的浮点数的值

阶码部分的二进制不全为1也不全为0。
尾数部分约定小数点的左边为1，即1.XXXXXXX，这是一种额外获得一个精度位的表示技巧。
IEEE 754没有要求原码的小数点的右边正数为1，负数为0，所以正常情况下，尾数的表示范围是[1,2)，因此规格化的浮点数不能表示那些非常接近0的数以及0。浮点数在计算机里面的表示形式是有限的、离散的、近似的，存在舍入误差，即只是实数的一个非常接近的子集。在一些精度要求非常高或者数值比较的场景，比较最好不要使用浮点数，会产生一些错误，主要原因是计算机二进制系统无法精确表示1/10，就好像十进制系统无法精确表示1/3。