【定义】
Lucas定理是用来求 C(n,m) mod p的值。条件:n和m是非负整数,p是素数
一般用于:n和m但p很小,或者n,m不大但大于p,这样用阶乘解决不了。
【公式】
表达式:C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p。(可以递归)
递归方程:(C(n%p, m%p)*Lucas(n/p, m/p))%p。(递归出口为m==0,return 1)
二进制推导:
将n,m(0~n) 化为二进制数
a,b为n,m的二进制数
根据定理 C(n,m)=C(a[n],b[n])*C(a[n-1],b[n-1])*...*C(a[0],b[0])
应用:HDU - 4349 Xiao Ming's Hope lucas
【例题+实现】
参考: https://blog.csdn.net/ACdreamers/article/details/8037918
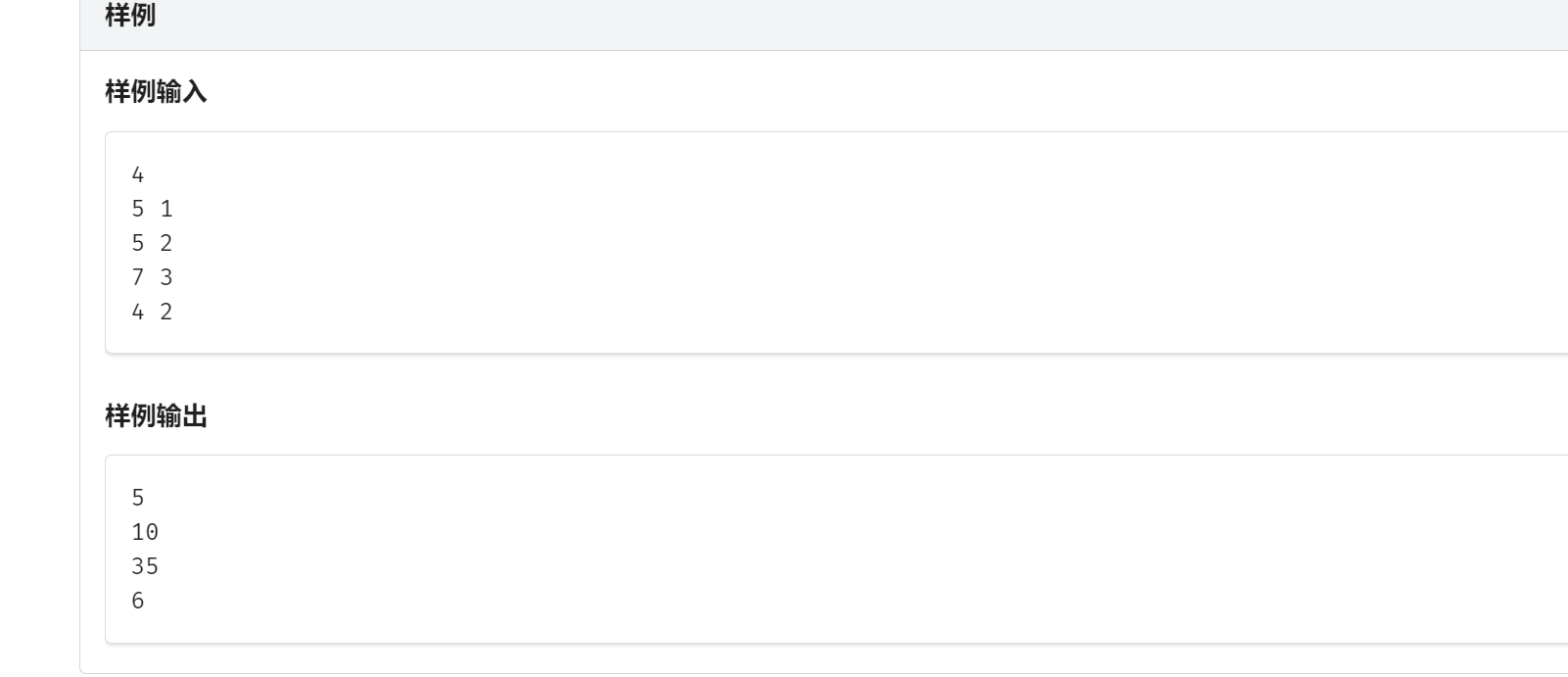
假如现在叫你求:C(n,m)mod p,0<=p<=1e10,且p为素数
代码模板:(超时已经修改)
using namespace std;
typedef long long ll;LL n,m,mod;
//适用于p很大
ll qpow(ll a,ll b)
{ll ans=1;while(b){if(b&1)ans=(ans*a)%mod;a=(a*a)%mod;b>>=1;}return ans;
}
ll getc(ll a,ll b)
{if(a<b)return 0;if(b>a-b)b=a-b;ll s1=1,s2=1;for(ll i=0;i<b;i++){s1=s1*(a-i)%mod;s2=s2*(i+1)%mod;}return s1*qpow(s2,mod-2)%mod;
}
ll lucas(ll n,ll k)
{if(k==0)return 1;return getc(n%mod,k%mod)*lucas(n/mod,k/mod)%mod;
}
由于上题的p比较大,所以组合数只能一个一个计算,如果p的范围小点,那么就可以进行阶乘预处理计算了。
1.p固定的时候,且范围较大,n,m范围不大
n (1 ≤ n ,m≤ 1e6), k (0 ≤ k ≤ n).T (≤ 2000) p为素数
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <queue>
#include <set>
#include <map>
#include <stack>
#include <string>
#include <vector>
#include <deque>
#include <list>
#include <functional>
#include <numeric>
#include <cctype>
using namespace std;
#define LL __int64
const int N=2000100;
const int p=1000000007;LL fac[N];void init() //预处理阶乘
{LL i;fac[0] =1;for(i =1; i < N; i++)fac[i] = fac[i-1]*i % p;
}LL exp_mod(LL a, LL b)
{LL tmp = a % p, ans =1;while(b){if(b & 1) ans = ans * tmp % p;tmp = tmp*tmp % p;b >>=1;}return ans;
}LL C(LL n, LL m)
{if(m > n)return 0;return fac[n]*exp_mod(fac[m]*fac[n-m], p-2) % p;//逆元
}LL Lucas(LL n, LL m)
{if(m ==0)return 1;return (C(n%p, m%p)*Lucas(n/p, m/p))%p;
}int main()
{int T;LL n,m,cas=1;init();scanf("%d",&T);while(T--){scanf("%lld %lld",&n,&m);printf("Case %lld: %lld\n",cas++,Lucas(n+m-1,m-1));}return 0;
}
2.HDU3944: http://acm.hdu.edu.cn/showproblem.php?pid=3944
1<=m<=n<=1e6和1<=p<=1e5,并且p可能为合数,
对于本题,由于访问的次数很大,所以当然得先预处理保存在数组中,然后用的时候就不用一次一次的再重复计算了,本题重在预处理。
#include <stdio.h>
#include <string.h>
#define N 10005 int p; int prim[N]; //保存素数
int pth[N]; //保存当前数是第几个素数
bool prime[N];
int fac[N][N];
int inv[N][N];
//这里的fac[i][j]和inv[i][j]表示prime[i]的阶乘mod p和它的逆元int k=0; void isprime() //质数打表
{ int i,j; memset(prime,true,sizeof(prime)); memset(pth,0,sizeof(pth)); for(i=2;i<N;i++) { if(prime[i]) { prim[++k]=i; pth[i]=k; for(j=i+i;j<N;j+=i) { prime[j]=false; } } }
} int quick_mod(int a,int b,int m) //快速幂
{ int ans=1; a%=m; while(b) { if(b&1) { ans=ans*a%m; b--; } b>>=1; a=a*a%m; } return ans;
} void init() //预处理阶乘数
{ int i,j; for(int i=1;i<=k;i++) { fac[i][0]=inv[i][0]=1; for(j=1;j<prim[i];j++) { fac[i][j]=(fac[i][j-1]*j)%prim[i]; inv[i][j]=quick_mod(fac[i][j],prim[i]-2,prim[i]); } } } int C(int n,int m)
{ if(m>n) return 0; if(m==n) return 1; int t=pth[p]; return fac[t][n]*(inv[t][n-m]*inv[t][m]%p)%p;
} int Lucas(int n,int m)
{ if(m==0) return 1; return C(n%p,m%p)*Lucas(n/p,m/p)%p;
} int main()
{ int n,m,k=1; isprime(); init(); while(~scanf("%d%d%d",&n,&m,&p)) { if(m<=n/2) m=n-m; printf("Case #%d: %d\n",k++,(m%p+Lucas(n+1,m+1)%p)%p); } return 0;
}