Run Run Run

学习了 2022 年集训队论文《浅谈与 Lyndon 理论有关的字符串组合问题》
写得很好，像我这样的字符串小白也能看懂

Lyndon 分解

若字符串 $w$ 小于它的每一个真后缀，则称 $w$ 是 Lyndon 串。
若字符串 $w$ 是 Lyndon 串，则 $w^kw'$ 是近似 Lyndon 串，其中 $w^{'}$ 是 $w$ 的前缀。

串 $w$ 可以分解位 $w_1^{c_1}\dots w_{k}^{c_k}$ ，其中 $w_1>\dots>w_k$ 。

最小后缀族：对于串 $w$ 的后缀 $w^{'}$ ，若存在 $u$ 使得任意后缀 $w^{''}$ 满足 $w^{'} u < w^{''} u$ ，则 $w^{'}$ 是 $w$ 的一个有效后缀，有效后缀的集合称为 $w$ 的最小后缀族，记为 $S S (w)$

若 $u^2v,uv,v$ 都是 $w$ 的后缀，则 $u v$ 不是有效后缀。
若 $u,v\in SS(w),|u|<|v|$ ，则 $u$ 是 $v$ 的 $b o r d e r$ ，且 $2|u|\le |v|$ 。
有效后缀形如 $s_i=w_i^{c_i}\dots w_k^{c_k}$
$s_{i+1}$ 是 $s_i$ 的前缀的充要条件是 $i\le \lambda$ ，其中 $s_{\lambda}$ 是对 $w$ 进行 Duval 算法时第一次比较完字符串末尾时的近似 Lyndon 后缀。（因为 $w_i^xs_{i+1}$ 是近似 Lyndon 后缀，所以 $s_{i+1}$ 是 $w_{i}$ 的前缀）

后接 $v$ 的最小后缀：

给定 $w, v$ ，求 $w$ 的后缀 $u$ ，使得 $u v$ 最小，记为 $M i n s u f (w, v)$

由于 $u$ 是 $s_{\lambda},\dots,s_k$ 之一，另 $w_i=s_{i+1}+y_i$ ， $x_i=y_i+s_{i+1}$ ，则有 $s_i=s_{i+1}+x_i^{c_i}$ 。

$\forall i\in [\lambda,k-1],y_i>x_{i+1}^{\infty}$ ，即证 $s_{i+1}y_i>s_{i+1}x_{i+1}^{\infty}$ ，即 $w_i>w_{i+1}^{\infty}s_{i+2}$ ，又有 $w_i>w_{i+1}^{\infty}$ 。
$\forall i\in [\lambda,k-1],x_i^{\infty}>x_{i+1}^{\infty}$

考虑比较 $s_iv$ 和 $s_{i+1}v$ 的大小，发现这等价与比较 $x_i^{c_i}v$ 和 $v$ 的大小，这等价于比较 $x_i^{\infty}$ 和 $v$ 的大小，故可以二分找到一个 $i$ 使得 $x_i^{\infty}>v>x_{i+1}^{\infty}$ ，此时 $Minsuf(w,v)=s_{i+1}v$ 。

例：JSOI 2019 节日庆典，求每个前缀的最小表示。
线性做法：考虑当前串可以表示成 $uw^kw'$ ，那么只需要考虑最小表示开头为 $w^kw'$ 或开头在 $w^{'}$ 里面的情况，在 $w^{'}$ 里面时发现去掉最后 $∣ w ∣$ 个字符即为 $uw^{k-1}w'$ 的循环表示，是之前已经求出的答案。

Runs

Runs 的定义和 Runs 定理

定义：本源串， $k$ 次方串，平方串，本源 $k$ 次方串。
Runs：对于字符串 $S$ ，若其一个子串 $S [i, j]$ 具有最小周期 $p$ ，满足 $2p\le j-i+1$ ，且 $S_{i-1}\neq S_{i+p-1}，S_{j+1}\neq S_{j+1-p}$ ，则 $r = (i, j, p)$ 构成 $S$ 的一个 run， $e_r=\frac{j-i+1}{p}$ 为它的指数， $S$ 的所有 runs 的集合记为 $R u n s (S)$ 。
Runs 为研究幂串结构提供了方法，容易发现我们定义的 runs 满足 run 里面至少有一个平方串。

周期相同的两个 runs 的交长度 $< p$ 。
任何一个 run $r = (i, j, p)$ 可以导出 $j - i + 1 - 2 p$ 个本源平方串，每个本源平方串由唯一一个 run 导出

下面，我们将证明两个重要的命题：
Runs 定理：记 $\rho(n)$ 和 $\sigma(n)$ 表示长为 $n$ 的串的 runs 个数以及 runs 指数和的最大值，有 $\rho(n)<n,\sigma(n)<3n$ 。

记 $_0,<_1$ 为字符集上两种相反的序。

定义 Lyndon 根：对于一个 run $r = (i, j, p)$ ，若在字典序 $<$ 下其长为 $p$ 的子串 $S [u, u + p - 1]$ 为 Lyndon 串，则称 $S [u, u + p - 1]$ 是 $r$ 关于 $<$ 的一个 Lyndon 根。
定义 Lyndon 数组：定义 $l_t(i)$ 表示在 $_t$ 下左端点为 $i$ 的最长 Lyndon 串的右端点，将 $l_t(i)$ 成为 $S$ 的 Lyndon 数组。
性质： $l_0(i),l_1(i)$ 恰有一个为 $i$ ，证明略。
性质：对于 run $r = (i, j, p)$ ，设 $S_{j+1}<_tS_{j+1-p}$ ，那么其任意 Lyndon 根 $S [u, u + p - 1]$ 有 $l_t(u)=u+p-1$ 。证明：对于 $S[u,v],u+p-1<v\le j$ 满足其为 $w^kw'$ ，对于 $v > j$ 显然不是 Lyndon 串。
定义 Lyndon 根：若 run $r = (i, j, p)$ 的 Lyndon 根 $S [u, u + p - 1]$ 满足 $u > i$ ，那么其为真 Lyndon 根。
性质： $S[u,l_0(u)],S[u,l_1(u)]$ 不可能同时为两个 run 的 Lyndon 根。证明：设 $l_0(u)=u$ ，则有 $S_u=S_{u-1}+S_{u+p-1}=S_{l_1(u)}$ ，故 $S[u,l_1(u)]$ 不是 Lyndon 串。
性质：任意两个不同的 run 的真 Lyndon 根左端点集合不交。（由上一条得到）

Runs 的求解方法

算法 1：枚举周期 $p$ ，用 NOI2016 优秀的拆分的做法解决。
算法 2：由于 runs 的 Lyndon 根一定形如 $S[i,l_t(i)]$ ，所以先求出 Lyndon 数组再进行扩展即可。求 Lyndon 数组可以考虑一种从后向前构造 Lyndon 分解的方法，即从后往前扫，维护一个单调栈，每次加入一个字符，检查能不能和栈顶的串合并。

幂串的结构

性质：若 $u^2,v^2,w^2$ 是本源平方串，且 $u^2$ 是 $v^2$ 的前缀， $v^2$ 是 $w^2$ 的前缀，则 $|w|\ge |u|+|v|$ 。

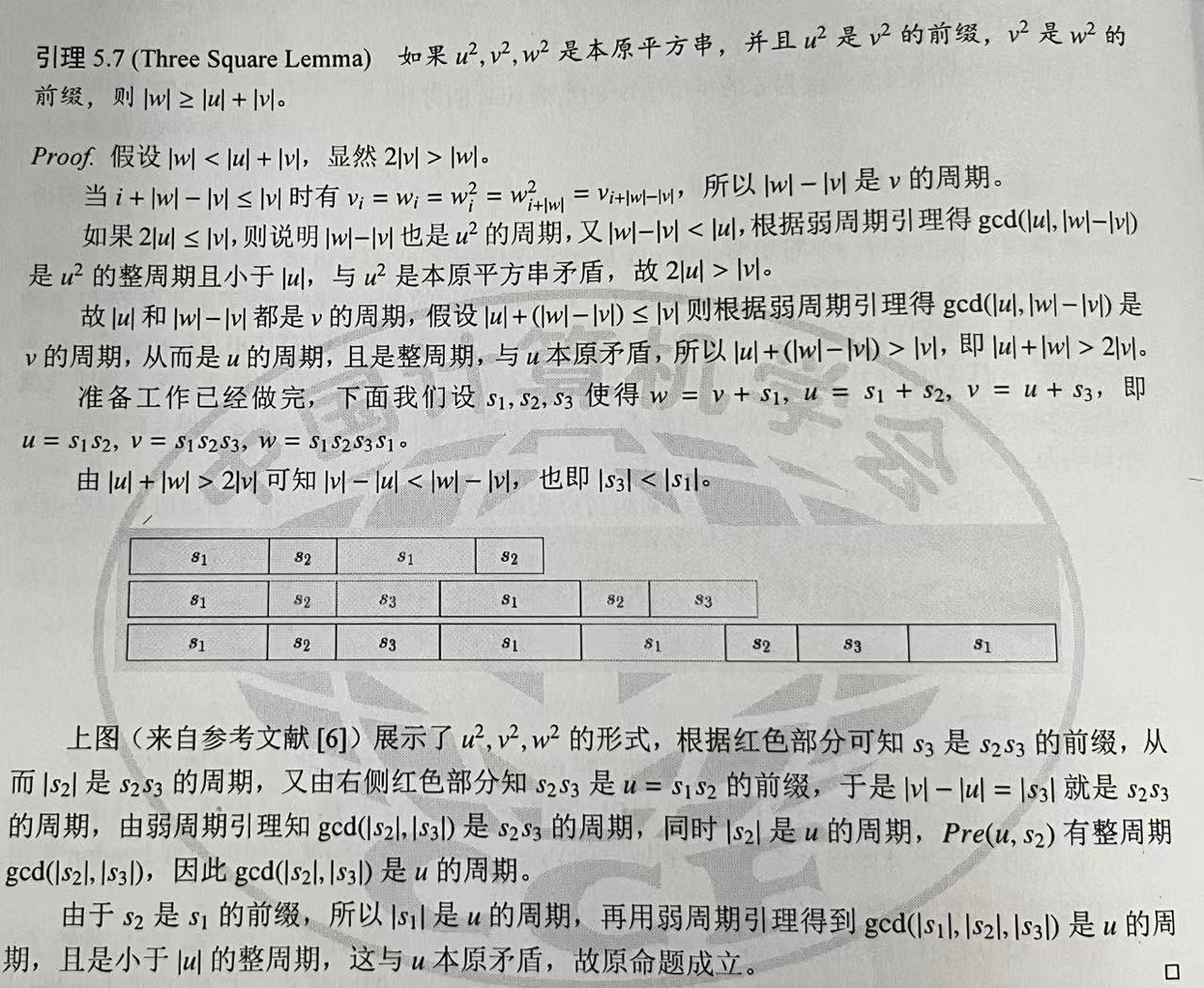
于是我们有结论：串 $w$ 的本源平方前缀个数为 $O(\log |w|)$ 个。
串 $w$ 的本源平方串个数为 $O(|w|\log |w|)$ 个，于是也有 $\sum_r （j-i+1-2p)$ 为 $O(|w|\log |w|)$ 。

性质：字符串 $w$ 的本质不同本源平方串个数为 $O (∣ w ∣)$ 。证明：考虑最后一次出现位置，假设一个左端点有 3 个 $u, v, w$ ，则有 $2|u|\le |w|$ ，那么 $u^2$ 不是最后一次出现。

例：ZJOI 2020 字符串，区间询问本质不同平方串。

先忽略本质不同，考虑 run $r = (i, j, p)$ ，其每个 $S [l, l + 2 k p - 1]$ 都可以作为一个贡献。将 $(l, l + 2 k p - 1)$ 看作一个点，那么对于一个 $k$ ，我们可以将操作看成斜线加，加的次数是 $\sum_r \frac{j-i+1}{p}$ ，其为 $O (n)$ 。
下面考虑本质不同，对于两个相同子串 $S [i, i + 2 p - 1], S [j, j + 2 p - 1]$ ，我们在 $(i, j + 2 p - 1)$ 放一个权值为 $- 1$ 的点即可。在一个 run 里面的同样只需要枚举 $k$ 然后斜线减，否则就是和前面一个 run 里面的相同。从做到右扫 runs，我们只关注 run 里面第一次出现的平方串，容易发现其个数为 $\sum_r (j-i+1-2p)\sim O(n\log n)$ ，故直接使用 hash，然后在平面上会添加 $O(n\log n)$ 个点。时间复杂度 $O(n\log^2 n+q\log n)$ 。

Lyndon 树

对于一个 Lyndon 串 $w$ ，我们可以得到一个 $2 ∣ w ∣ - 1$ 个结点的二叉树，每个结点代表一个子串（且也为 Lyndon 串），构建的方法为找到 $w = u + v$ ，其中 $v$ 是 $w$ 的最小后缀，然后 $u, v$ 为 $w$ 的两个儿子。

构建方法：从后向前，维护 $[i + 1, n]$ 组成的森林（每一个子树是一个 Lyndon 串），加入当前字符 $S_i$ ，会合并栈顶的一些 Lyndon 串，将这些点串起来即可。

性质：以 $i$ 为左端点的最长 Lyndon 子串对应 Lyndon 树中以 $i$ 为左端点的最大子树。（证明：建树的过程和求 Lyndon 数组相同）
性质：若 $S [l, r]$ 是 Lyndon 串，则 $l,\dots,r$ 的 LCA 的子树的左端点为 $l$ 。

区间短周期查询：每次查询 $S [l, r]$ 的最小周期，若最小周期大于一半则不用输出。

这等价与查询是否有一个包含 $[l, r]$ 且周期不超过 $\frac{r-l+1}{2}$ 的 run。
以 $_0,<_1$ 两种比较关系建 Lyndon 树，分别求出 $l,\dots,\lceil \frac{l+r}{2}\rceil$ 的 LCA，检查以其右子树为 Lyndon 根的 runs。
证明：我们只需要找到一个包含 $m$ 的 Lyndon 根。 LCA 的右子树 $x$ 满足条件，若其不为答案的 runs $r = (i, j, p)$ ，那么我们知道 $x$ 的右端点大于 $j$ ，但是 $S_{j+1}<S_{j+1-p}$ ，这与 $x$ 的子树是 Lyndon 串矛盾。

Lyndon 串计数

记 $\hat w$ 为 $w$ 的最小表示，若 $\hat w=w$ 则称 $w$ 为 necklace。
性质：每个 Lyndon 串都是 necklace，每个 necklace 可以写成 $w^k$ 其中 $w$ 是 Lyndon 串。

$\hat w$ 的求法：首先找到 $u^k=w$ 然后求 $\hat u$ ，只需要对 $u u$ 求 Lyndon 分解，然后找到最后一个在 $[1, ∣ u ∣]$ 中分解的地方 $x$ ，那么 $\hat u=u[x,|u|]+u[1,x-1]$ 。

求前驱 necklace：求长度等于 $∣ w ∣$ 字典序 $\le w$ 的最大的 necklace。记作 $P L (w)$

$P L (w)$ 形如 $Pre(w,i-1)+P(w_i)+z^{|w|-i}$ ，其中 $P (c)$ 表示比 $c$ 小的最大字符，故我们有 $w|^2$ 的做法，即每次判断是不是 necklace。
考虑优化判断的过程，只需要判断 $Pre(w,i-1)+P(w_i)$ 是不是近似 Lyndon 串即可，用一次 Duval 算法就可以解决。

Lyndon 串计数：
设 $P (n), L (n)$ 表示本源串和 Lyndon 串的数量，有 $L(n)=\frac 1n P(n)$ ，且 $\Sigma^n=\sum _{d\mid n}P(d)$ ，那么 $L(n)=\frac 1n \sum_{d\mid n}\mu(\frac nd)\Sigma^d$ 。

Lyndon 串排名：
设 $P (d), P^{'} (d)$ 表示满足 $\hat u^{n/d}\le w$ 的任意串 $u$ 的数量，以及本源串 $u$ 的数量。
$rank=\frac 1nP'(n),P(x)=\sum_{d\mid x}P'(d)\to rank=\frac 1n\sum_{d\mid n} \mu(\frac nd)\times P(d)$ 。
容易发现 $P (d)$ 等价与 $\hat u\le Pre(w,d)$ 的任意串数量。
识别自动机： KMP 的改版，当转移字符等于 $w_i$ 时，到 $i + 1$ ，小于 $w_i$ 时到 $n$ ，否则到 0。

性质： $w$ 是 necklace， $\hat u\le w,|u|=|w|=n$ 当且仅当 $u^{2}$ 中存在一个不为 $w$ 真前缀的子串 $v$ 满足 $v\le w$ 。
性质： 发现对于 necklace 的识别自动机，它和 KMP 自动机一样。

对于计算 $P (n)$ ，我们只需要考虑不能转移到 $n$ 的点有多少，我们会发现，考虑串 $u^{\infty}$ 对于充分打大的 $j$ ， $j$ 转移到的点和 $j + ∣ u ∣$ 转移到的是一样的。
我们定义 $j ∣ u ∣$ 转移到的点 $t$ 为这个串的起始点，现在就是要求环的数量。设 $f_j$ 为长为 $j$ 的环的数量，枚举第一个环 $j$ ，有 $f_i=\sum_{j=1}^{min(n-1,i)} b_jf_{i-j}$ ，其中 $b_j$ 表示从这个点转移到 0 的边数。容易发现可以使用多项式求逆来解决。于此同时，答案为 $\sum_{i=1}^{n-1} i\times b_i\times f_{n-i}$ 。注意到也可以使用线性递推做到 $O(n\log n\log m)$ 的复杂度。