知识点

一 . nim游戏的数学定义

Nim游戏是博弈论中最经典的模型，它又有着十分简单的规则和无比优美的结论。
Nim游戏是组合游戏(Combinatorial Games)的一种，准确来说，属于“Impartial Combinatorial Games”（以下简称ICG）。

一般而言，满足以下条件的游戏是ICG：

有两名选手；
两名选手交替对游戏进行移动(move)，每次一步，选手可以在（一般而言）有限的合法移动集合中任选一种进行移动；
对于游戏的任何一种可能的局面，合法的移动集合只取决于这个局面本身，不取决于轮到哪名选手操作、以前的任何操作、骰子的点数或者其它什么因素；
如果轮到某名选手移动，且这个局面的合法的移动集合为空（也就是说此时无法进行移动），则这名选手失败。根据这个定义，很多日常的游戏并非ICG。例如象棋就不满足条件3，因为红方只能移动红子，黑方只能移动黑子，合法的移动集合取决于轮到哪名选手操作。

对于条件3，有更进一步的定义Position。

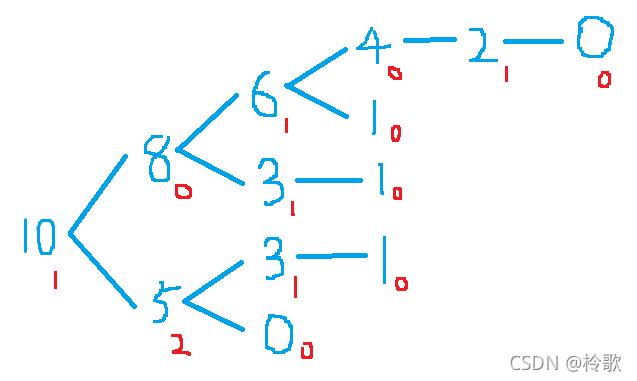
我们将Position分为两类：
P-position：在当前的局面下，先手必败。
N-position：在当前的局面下，先手必胜。

他们有如下性质：
1.合法操作集合为空的局面是P-position；
2.可以移动到P-position的局面是N-position；
3.所有移动都只能到N-position的局面是P-position。

重要结论：对于一个Nim游戏的局面 $(a_1,a_2,...,a_n)$ ，它是P-position时，当且仅当 $a_1$ ^ $a_2$ ^...^ $a_n$ =0；它是N-position时，当且仅当 $a_1$ ^ $a_2$ ^...^ $a_n$ !=0，其中^表示异或(xor)运算。

模板题：洛谷 P2197 【模板】nim 游戏

题目描述

甲，乙两个人玩 nim 取石子游戏。

nim 游戏的规则是这样的：地上有 n 堆石子（每堆石子数量小于 $10^4$ ），每人每次可从任意一堆石子里取出任意多枚石子扔掉，可以取完，不能不取。每次只能从一堆里取。最后没石子可取的人就输了。假如甲是先手，且告诉你这 n 堆石子的数量，他想知道是否存在先手必胜的策略。

输入格式

本题有多组测试数据。

第一行一个整数 T （ $T\leqslant 10$ ），表示有 T 组数据

接下来每两行是一组数据，第一行一个整数 n，表示有 n 堆石子， $n\leqslant 10^4$ 。

第二行有 n 个数，表示每一堆石子的数量.

输出格式

共 T 行，每行表示如果对于这组数据存在先手必胜策略则输出 Yes，否则输出 No。

输入输出样例

输入 #1

输出 #1

No
Yes

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
inline int read()
{int x=0,f=1;char c=getchar();while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}while(c>='0' && c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}return x*f;
}int main()
{int t=read();for(int i=1;i<=t;++i){int n=read(),res;for(int j=1;j<=n;++j){int a=read();if(j == 1) res=a; //将第一个数记录在res中else res^=a; //后添加的数与前面的数不断异或}if(res == 0) printf("No\n");else printf("Yes\n");}
}