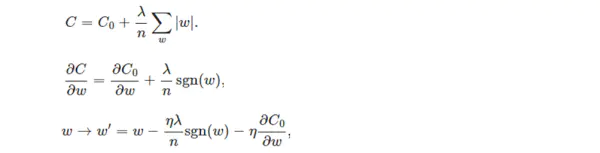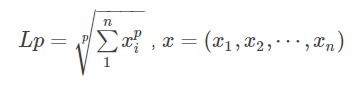【转】浅谈流形学习

转自：http://www.sigvc.org/bbs/thread-800-1-1.html

总觉得即使是“浅谈”两个字，还是让这个标题有些过大了，更何况我自己也才刚刚接触这么一个领域。不过懒得想其他标题了，想起来要扯一下这个话题，也是因为和朋友聊起我自己最近在做的方向。Manifold Learning 或者仅仅 Manifold 本身通常就听起来颇有些深奥的感觉，不过如果并不是想要进行严格的理论推导的话，也可以从许多直观的例子得到一些感性的认识，正好我也就借这个机会来简单地谈一下这个话题吧，或者说至少是我到目前为止对这它的认识。
这两个词，在谈 Manifold 之前，不妨先说说 Learning ，也就是 Machine Learning 。而说道 Machine Learning 而不提一下 Artificial Intelligence 的话似乎又显得有些不厚道。人说 AI 是一门最悲剧的学科，因为每当它的一个子领域发展得像模像样之后，就立马自立门户，从此和 AI “再无瓜葛”了，而 Machine Learning 大概要算是最新的一个典型吧。这就让人有点奇怪，比如说数学，分门别类总算是够多了吧？可以不管怎么分，大家兄弟姐妹也都还承认自己是叫“数学”的。那 AI 呢？我觉得这里有很大一部分是它自身定位的问题。
反正现在我是不太清楚 AI 是做什么的，不知道其他人到底清楚不清楚。Wikipedia 上说

Artificial intelligence (AI) is the intelligence of machines and the branch of computer science that aims to create it.

可是这相当于一个 tautology ，因为到底什么又是 the intelligence of machines 呢？一开始的时候，大牛们都野心勃勃，而且好像也是信心满满，就好像曾经广泛认为“牛顿定理揭示了宇宙真理，科学剩下的事情只要按照公式来做计算就可以了”一样，大家可能觉得，不出几十年，人类就可以不用思考，交给 AI 来做了。不过我这里并不想再多说诸如什么是“思考”，什么是“智能”之类的以及随之而来的“图灵测试”之类的话题。我想说的是，到头来，AI 到底是什么，这还是一个问题，或者说，AI 在一开始定了一个过高的目标，几十年后，发现情况并不像当年那么乐观，却又有些下不了台了。
这个时候，AI 的一些旁枝或者子领域果断放下面子，丢掉了那个近乎玄幻的目标，逐渐发展成为“正常”的学科，所以也就不再好称为 AI 了。或者说现在的 AI 有两个意思，一个广义的 AI ，包括了所有相关的以及派生的领域，另一个则是狭义的或者经典的 AI ，专门指那些仍然在执着地追求着真正的“智能”的部分，或者说得不好听一点，就是剩下的部分。
Machine Learning 作为离家出走的典型，虽然名字里带了 Learning 一个词，让人乍一看觉得和 Intelligence 相比不过是换了个说法而已，然而事实上这里的 Learning 的意义要朴素得多。我们来看一看 Machine Learning 的典型的流程就知道了，其实有时候觉得和应用数学或者更通俗的数学建模有些类似，通常我们会有需要分析或者处理的数据，根据一些经验和一些假设，我们可以构建一个模型，这个模型会有一些参数（即使是非参数化方法，也是可以类似地看待的），根据数据来求解模型参数的过程，就叫做 Parameter Estimation ，或者 Model Fitting ，但是搞机器学习的人，通常把它叫做 Learning （或者，换一个角度，叫 Training）——因为根据数据归纳出一个有用的模型，这和我们人类“学习”的过程还是挺类似的吧。不过，如果抛开无聊的抠字眼游戏的话，我们可以看到，Machine Learning 已经抛弃了“智能”的高帽子，它的目的就是要解决具体的问题——而并不关心是否是通过一种“智能”的方式类解决的。
说到这里，其实我们构造模型就类似于写一个类，数据就是构造函数的参数，Learning 就是构造函数运行的过程，成功构造一个对象之后，我们就完成了学习。一些 Machine Learning 的问题到这一步就结束了，另一些情况还会使用得到的模型（对象）对后来的数据进行一些处理，通常会是 Inferencing 。到这个时候，又有些像统计里的东西了，所谓“统计推断”嘛。其实原本统计和机器学习研究的不少问题就是交叉在一起的，不过两派人从不同的角度来看待同样的问题。而且，也确实有 Statistical Learning 这么一个说法存在的，可以把他看成是 Machine Learning 的一个子领域（或者是一个分子或者甚至就是 Machine Learning 本身）。
<ignore_js_op> 
到这里，如果你还没有因为不断地抠字眼而烦躁的话，我已经忍无可忍了。所以，我就假定你已经了解了什么叫 Learning ，或者是已经恶心到懒得去了解了。于是我们转入下一个话题：流形，也就是 Manifold 。不知道你有没有为我在本文开头放上的那个地球的图片感到困惑？这是因为球面是一个很典型的流形的例子，而地球就是一个很典型的“球面”啦（姑且当作球面好啦）。
有时候经常会在 paper 里看到“嵌入在高维空间中的低维流形”，不过高维的数据对于我们这些可怜的低维生物来说总是很难以想像，所以最直观的例子通常都会是嵌入在三维空间中的二维或者一维流行。比如说一块布，可以把它看成一个二维平面，这是一个二维的欧氏空间，现在我们（在三维）中把它扭一扭，它就变成了一个流形（当然，不扭的时候，它也是一个流形，欧氏空间是流形的一种特殊情况）。
所以，直观上来讲，一个流形好比是一个 d 维的空间，在一个 m 维的空间中 (m > d) 被扭曲之后的结果。需要注意的是，流形并不是一个“形状”，而是一个“空间”，如果你觉得“扭曲的空间”难以想象，那么请再回忆之前一块布的例子。如果我没弄错的话，广义相对论似乎就是把我们的时空当作一个四维流（空间三维加上时间一维）形来研究的，引力就是这个流形扭曲的结果。当然，这些都是直观上的概念，其实流形并不需要依靠嵌入在一个“外围空间”而存在，稍微正式一点来说，一个 d 维的流形就是一个在任意点出局部同胚于（简单地说，就是正逆映射都是光滑的一一映射）欧氏空间  。
<ignore_js_op> 
实际上，正是这种局部与欧氏空间的同胚给我们带来了很多好处，这使得我们在日常生活中许许多多的几何问题都可以使用简单的欧氏几何来解决，因为和地球的尺度比起来，我们的日常生活就算是一个很小的局部啦——我突然想起《七龙珠》里的那个界王住的那种私人小星球，走几步就要绕一圈的感觉，看来界王不仅要体力好（那上面重力似乎是地球的十倍），而且脑力也要好，初中学的必须是黎曼几何了！
那么，除了地球这种简单的例子，实际应用中的数据，怎么知道它是不是一个流形呢？于是不妨又回归直观的感觉。再从球面说起，如果我们事先不知道球面的存在，那么球面上的点，其实就是三维欧氏空间上的点，可以用一个三元组来表示其坐标。但是和空间中的普通点不一样的是，它们允许出现的位置受到了一定的限制，具体到球面，可以可以看一下它的参数方程：
<ignore_js_op> 可以看到，这些三维的坐标实际上是由两个变量  和  生成的，也可以说成是它的自由度是二，也正好对应了它是一个二维的流形。有了这样的感觉之后，再来看流形学习里经常用到的人脸的例子，就很自然了。下图是 Isomap 论文里的一个结果：
<ignore_js_op> 
这里的图片来自同一张人脸（好吧，其实是人脸模型），每张图片是 64×64 的灰度图，如果把位图按照列（或行）拼起来，就可以得到一个 4096 维的向量，这样一来，每一张图片就可以看成是 4096 维欧氏空间中的一个点。很显然，并不是 4096 维空间中任意一个点都可以对应于一张人脸图片的，这就类似于球面的情形，我们可以假定所有可以是人脸的 4096 维向量实际上分布在一个 d 维 (d < 4096) 的子空间中。而特定到 Isomap 的人脸这个例子，实际上我们知道所有的 698 张图片是拍自同一个人脸（模型），不过是在不同的 pose 和光照下拍摄的，如果把 pose （上下和左右）当作两个自由度，而光照当作一个自由度，那么这些图片实际只有三个自由度，换句话说，存在一个类似于球面一样的参数方程（当然，解析式是没法写出来的），给定一组参数（也就是上下、左右的 pose 和光照这三个值），就可以生成出对应的 4096 维的坐标来。换句话说，这是一个嵌入在 4096 维欧氏空间中的一个 3 维流形。
实际上，上面的那张图就是 Isomap 将这个数据集从 4096 维映射到 3 维空间中，并显示了其中 2 维的结果，图中的小点就是每个人脸在这个二维空间中对应的坐标位置，其中一些标红圈的点被选出来，并在旁边画上了该点对应的原始图片，可以很直观地看出这两个维度正好对应了 pose 的两个自由度平滑变化的结果。
就我目前所知，把流形引入到机器学习领域来主要有两种用途：一是将原来在欧氏空间中适用的算法加以改造，使得它工作在流形上，直接或间接地对流形的结构和性质加以利用；二是直接分析流形的结构，并试图将其映射到一个欧氏空间中，再在得到的结果上运用以前适用于欧氏空间的算法来进行学习。
这里 Isomap 正巧是一个非常典型的例子，因为它实际上是通过“改造一种原本适用于欧氏空间的算法”，达到了“将流形映射到一个欧氏空间”的目的。  
Isomap 所改造的这个方法叫做 Multidimensional Scaling (MDS) ，MDS 是一种降维方法，它的目的就是使得降维之后的点两两之间的距离尽量不变（也就是和在原是空间中对应的两个点之间的距离要差不多）。只是 MDS 是针对欧氏空间设计的，对于距离的计算也是使用欧氏距离来完成的。如果数据分布在一个流形上的话，欧氏距离就不适用了。
让我们再回到地球——这个在三维空间中的二维流形，假设我们要在三维空间中计算北极点和南极点的距离，这很容易，就是两点相连的线段的长度，可是，如果要在这个流形上算距离就不能这样子算了，我们总不能从北极打个洞钻到南极去吧？要沿着地球表面走才行，当然，如果我随便沿着什么路线走一遍，然后数出总共走了多少步作为距离，这是不成的，因为这样一来如果我沿着不同的路线走，岂不是会得到不同的距离值？总而言之，我们现在需要一个新的定义在地球表面（流形）上的距离度量，理论上来说，任意满足测度的 4 个条件的函数都可以被定义为距离，不过，为了和欧氏空间对应起来，这里选择一个直线距离的推广定义。
还记得初中学的“两点之间，线段最短”吗？现在，我们反过来说，把线段的概念推广一下，变成“两点之间最短的曲线是线段”，于是流形上的距离定义也就等同于欧氏空间了：流形上两个点之间的距离就是连接两个点的“线段”的长度。虽然只是置换了一个概念，但是现在两者统一起来了，不过，在流形上的线段大概就不一定是“直”的了（于是直线也变成不一定是“直”的了），通常又称作是“测地线”。对于球面这个简单的流形来说，任意一条线段必定是在一个“大圆”上的，于是球面上的直线其实都是一些大圆，也造成了球面这个流形上没有平行线等一系列尴尬的局面（任意两条直线均相交），如果你看过一些数学科普八卦类的书，应该会回忆起不少东西啦！
回到 Isomap ，它主要做了一件事情，就是把 MDS 中原始空间中距离的计算从欧氏距离换为了流形上的测地距离。当然，如果流形的结构事先不知道的话，这个距离是没法算的，于是 Isomap 通过将数据点连接起来构成一个邻接 Graph 来离散地近似原来的流形，而测地距离也相应地通过 Graph 上的最短路径来近似了。如下图所示：
<ignore_js_op> 
这个东西叫做 Swiss Roll ，姑且把它看作一块卷起来的布好了。图中两个标黑圈的点，如果通过外围欧氏空间中的欧氏距离来计算的话，会是挨得很近的点，可是在流形上它们实际上是距离很远的点：红色的线是 Isomap 求出来的流形上的距离。可以想像，如果是原始的 MDS 的话，降维之后肯定会是很暴力地直接把它投影到二维空间中，完全无视流形结构，而 Isomap 则可以成功地将流形“展开”之后再做投影。
除了 Isomap 之外，Manifold Embedding 的算法还有很多很多，包括 Locally Linear Embedding 、Laplacian Eigenmaps 、Hessian Eigenmaps 、Local Tangent Space Alignment、Semidefinite Embedding (Maximum Variance Unfolding) 等等等等。哪个好哪个坏也不好说，它们都各有特点，而且也各自有不少变种。网上有一个 Matlab 的 demo ，给出了几种流行的 manifold embedding 算法在一些 synthetic manifold 上的结果和对比，可以有一个直观的认识。
另一方面是改造现有算法使其适合流形结构甚至专门针对流形的特点来设计新的算法，比较典型的是 graph regularized semi-supervised learning 。简单地说，在 supervised learning 中，我们只能利用有 label 的数据，而（通常都会有很多的）没有 label 的数据则白白浪费掉。在流形假设下，虽然这些数据没有 label ，但是仍然是可以有助于 Learn 出流形的结构的，而学出了流形结构之后实际上我们就是对原来的问题又多了一些认识，于是理所当然地期望能得到更好的结果喽。
当然，所有的这些都是基于同一个假设，那就是数据是分布在一个流形上的（部分算法可能会有稍微宽松一些的假设），然而 real world 的数据，究竟哪些是分别在流形上的呢？这个却是很难说。不过，除了典型的 face 和 hand written digit 之外，大家也有把基于流形的算法直接用在诸如 text 看起来好像也流形没有什么关系的数据上，效果似乎也还不错。
话说回来，虽然和实际应用结合起来是非常重要的一个问题，但是也并不是决定性的，特别是对于搞理论方面的人来说。

我想，对于他们来说，其实也像是在做应用啦，不过是把数学里的东西应用到机器学习所研究的问题里来，而且其中关系错综复杂，图论、代数、拓扑、几何……仿佛是十八路诸侯齐聚一堂，所以让我总觉得要再花 500 年来恶补数学才行呀！
不过我表示可以理解其中存在的潜在的 happy 之处，就好比你玩游戏，先玩了《天地劫：神魔至尊传》，然后再玩《天地劫序章：幽城幻剑录》的时候，会发现里面的人物、剧情逐渐地联系起来，也许甚至只是在一个地方出现过的一个完全不起眼的配角，当你再在另一地方突然看到他是，一系列的线索瞬间被联系起来，全局的画面渐渐浮现，那种 happy 的感觉，大概就是所谓的“拨云见日”了吧！  
所以呀，这些东西其实都是差不多的，有时候想想那些泰斗站在顶峰上“一览众山小”的感觉，那种“融会贯通”的感觉，真是让人各种羡慕呀！无奈就只好去爬爬老和山北高峰来体验体验了。  
最后是总结：所谓 Machine Learning 里的 Learning ，就是在建立一个模型之后，通过给定数据来求解模型参数。而 Manifold Learning 就是在模型里包含了对数据的流形假设。嗯，还有什么？还有就是，我画的坐在楼兰古城城墙上的冰璃，一点都不像…… >_< 幽城迷不要砍我……
Update 2011.02.28: 根据留言里的信息，“流形”这个中文词取自文天祥的“天地有正气，杂然赋流形”，这个词第一次作为当前的数学意义使用是由北大数学系的一位老教授江泽涵老先生。老先生是我国代数拓扑学的开拓者。还是 caszgh 同学的导师的大学时代的老师。