一个数如果恰好等于它的因子之和，这个数就称为 "完数 "。例如6=1＋2＋3，编程找出1000以内的所有完数。

分析过程

• 所谓完数，就是其因子之和（不包括自己本身）等于其本身，称其为完数；
• 解决此题，我们需要将每个数逐个进行判断，如果条件符合，我们打印其因子就OK啦！
• 兼顾到程序时间复杂度，我们只需要判断**“1到该数的平方根”**就OK啦，但是我们需要将在此范围内对应的另一个因子算出来，即用原数除以此范围中该数的因子。比如题目中给出的6是完数，但是6的平方根为2(我们用转化为int类型)，但是我们都知道3也是6的因子，但是3又不在我们给出的范围【1，2】，我们只需要用6/2即可得到它。
• 这样做完我们在判断因子之和的时候，需要减去其本身一次，因为1是每个数的因子么，但是我们又求出了它的另一半，这又不符合完数的定义，所以我们在此必须减去其本身一次，即可得到正解！做到这一步，我们基本上就可以很容易的把代码写出来了！

代码展示

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#define M 1000int main()
{int i,j;for(i=2;i<M;i++){	int sum=0;for(j=1;j<=sqrt(i);j++){if((i%j)==0){sum=sum+j+(i/j);}}//判断是否为完全数，如果是，则打印其因子 if(i==sum-i){printf("%d is factors number: ",i);for(j=1;j<i;j++){	if(i%j==0)printf("%d ",j);}	printf("\n");}			}return 0;
}

运行结果展示

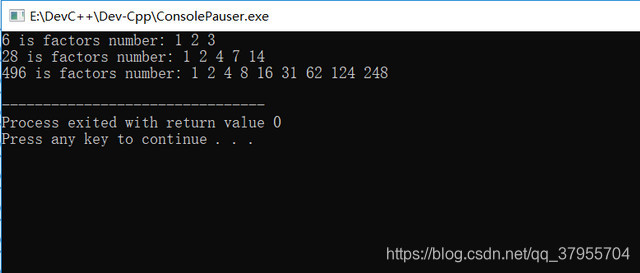
程序反思

小编对此代码的时间复杂度较为满意的，刚开始小编是从1到 i-1 来求其因子的，这样光判断是否为合数时间复杂度就已经基本为M^M了，小编这个代码的时间复杂度为M*sqrt(M),相比起前者，时间复杂度得到了更好的优化。大家可以将M的值给到100000就能很清楚的感受到了。
因为时间原因，后期小编再为大家提供另一种解决思路，今天举出来的解法时间复杂度还是有点大，我们应该寻找更优的解法，大家也可以留言谈谈你对此题的高见！欢迎大家批评留言及讨论！