概述在上一篇文章中讲到顺序存储二叉树,一般是用于完全二叉树,通过统一的数学公式可以将数组还原成完全二叉树
而对于普通的二叉树来说,也可以根据前序、中序和后序遍历得到的数组,还原二叉树
还原还原的情况分两种,分别是根据前序、中序和根据中序、后序
采用的二叉树如下图所示: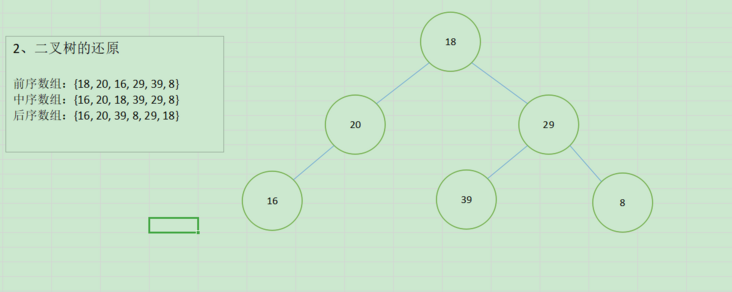
注意:前序和后序是没有办法还原二叉树
根据前序、中序还原二叉树如下图所示: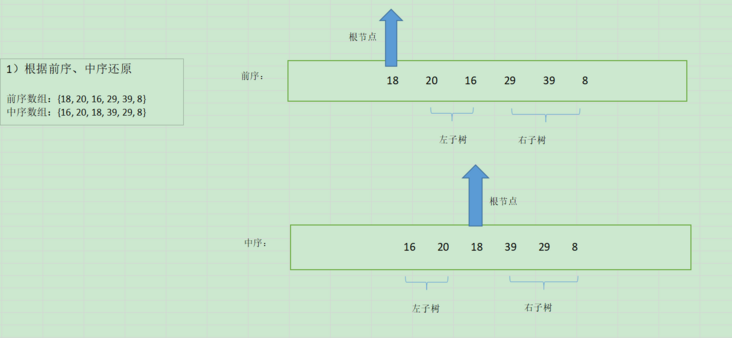
基本思路:根据前序数组,我们能够确定根节点(因为前序数组的根节点一定是第一个)
中序数组根据根节点能够确定左右子树的位置。(因为中序数组的根节点一定能够分开左右子树)
前序数组根据中序数组的左右子树的位置,也能够确定自己根节点的左右子树的位置(这部分可以看看代码怎么写的)
然后再分别递归左子树的前序、中序以及右子树的前序、中序,直到最后左右子树的长度都为0
代码如下:/**
* * @param pre 前序数组
* @param middle 中序数组
* @return 返回根节点
*/
public static TreeNode buildTree(int[] pre, int[] middle){
if (pre == null || middle == null || pre.length == 0 || middle.length == 0 || pre.length != middle.length)
return null;
//首先找到根节点
TreeNode root = new TreeNode(pre[0]);
//根据根节点的值找到中序遍历中的根节点的位置索引
int rootIndex = getIndex(middle, root.val);
if (rootIndex == -1)
return null;
//找到前序和中序中的左子树
//copyOfRange:拷贝[from, to)区间里的数据,左闭右开
int[] leftMiddle = Arrays.copyOfRange(middle, 0, rootIndex);
int[] leftPre = Arrays.copyOfRange(pre, 1, rootIndex + 1);
//找到前序和中序中的右子树
int[] rightMiddle = Arrays.copyOfRange(middle, rootIndex + 1, middle.length);
int[] rightPre = Arrays.copyOfRange(pre, rootIndex + 1, pre.length);
//用递归再次构建左右子树
TreeNode left = buildTree(leftPre, leftMiddle);
TreeNode right = buildTree(rightPre, rightMiddle);
//将左右子树添加到根节点上
root.left = left;
root.right = right;
return root;
}
根据中序、后序还原二叉树根据中序、后序和根据前序、中序是一样的道理,只不过是根节点从前序的第一个变为后序的最后一个,如下图所示: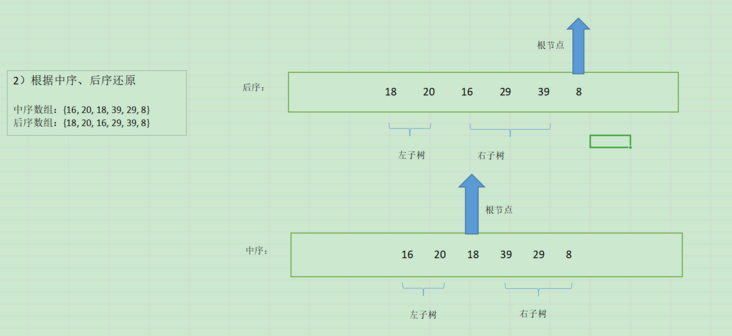
代码如下://根据中序和后序还原二叉树
/**
* * @param middle 中序数组
* @param last 后序数组
* @return 根节点
*/
public static TreeNode buildTree2(int[] middle, int[] last){
if (middle == null || last == null) return null;
int middleLen = middle.length; //获取中序数组的长度
int lastLen = last.length; //获取后序数组的长度
if (middleLen == 0 || lastLen == 0) return null;
//首先根据后序获取根节点
TreeNode root = new TreeNode(last[lastLen - 1]);
//根据root获取中序的根节点的索引值
int rootIndex = getIndex(middle, root.val);
if (rootIndex == -1)
return null;
//找到中序和后序的左子树
int[] leftMiddle = Arrays.copyOfRange(middle, 0, rootIndex);
int[] leftLast = Arrays.copyOfRange(last, 0, rootIndex);
//找到中序和后序的右子树
int[] rightMiddle = Arrays.copyOfRange(middle, rootIndex + 1, middleLen);
int[] rightLast = Arrays.copyOfRange(last, rootIndex, lastLen - 1);
//用递归再次构建左子树和右子树
TreeNode left = buildTree2(leftMiddle, leftLast);
TreeNode right = buildTree2(rightMiddle, rightLast);
//将左右子树添加到根节点
root.left = left;
root.right = right;
return root;
}
总体代码//树节点:
public class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val){
this.val = val;
}
}
//还原代码:
public class Travel {
public static void preorder_Traversal(TreeNode node){
if (node == null)
return;
System.out.println(node.val);
preorder_Traversal(node.left);
preorder_Traversal(node.right);
}
public static void inorder_Traversal(TreeNode node, int val){
if (node == null)
return;
inorder_Traversal(node.left, val);
System.out.println("---" + node.val);
if (node.val == val){
System.out.println("找到了:" + node.val);
return ; }
inorder_Traversal(node.right, val);
}
public static void postorder_Traversal(TreeNode node){
if (node == null)
return;
postorder_Traversal(node.left);
postorder_Traversal(node.right);
System.out.println(node.val);
}
public static int getIndex(int[] arr, int target){
for (int i = 0; i < arr.length; i ++){
if (arr[i] == target){
return i;
}
}
return -1;
}
//根据前序和中序还原二叉树
/**
* * @param pre 前序数组
* @param middle 中序数组
* @return 返回根节点
*/
public static TreeNode buildTree(int[] pre, int[] middle){
if (pre == null || middle == null || pre.length == 0 || middle.length == 0 || pre.length != middle.length)
return null;
//首先找到根节点
TreeNode root = new TreeNode(pre[0]);
//根据根节点的值找到中序遍历中的根节点的位置索引
int rootIndex = getIndex(middle, root.val);
if (rootIndex == -1)
return null;
//找到前序和中序中的左子树
//copyOfRange:拷贝[from, to)区间里的数据,左闭右开
int[] leftMiddle = Arrays.copyOfRange(middle, 0, rootIndex);
int[] leftPre = Arrays.copyOfRange(pre, 1, rootIndex + 1);
//找到前序和中序中的右子树
int[] rightMiddle = Arrays.copyOfRange(middle, rootIndex + 1, middle.length);
int[] rightPre = Arrays.copyOfRange(pre, rootIndex + 1, pre.length);
//用递归再次构建左右子树
TreeNode left = buildTree(leftPre, leftMiddle);
TreeNode right = buildTree(rightPre, rightMiddle);
//将左右子树添加到根节点上
root.left = left;
root.right = right;
return root;
}
//根据中序和后序还原二叉树
/**
* * @param middle 中序数组
* @param last 后序数组
* @return 根节点
*/
public static TreeNode buildTree2(int[] middle, int[] last){
if (middle == null || last == null) return null;
int middleLen = middle.length; //获取中序数组的长度
int lastLen = last.length; //获取后序数组的长度
if (middleLen == 0 || lastLen == 0) return null;
//首先根据后序获取根节点
TreeNode root = new TreeNode(last[lastLen - 1]);
//根据root获取中序的根节点的索引值
int rootIndex = getIndex(middle, root.val);
if (rootIndex == -1)
return null;
//找到中序和后序的左子树
int[] leftMiddle = Arrays.copyOfRange(middle, 0, rootIndex);
int[] leftLast = Arrays.copyOfRange(last, 0, rootIndex);
//找到中序和后序的右子树
int[] rightMiddle = Arrays.copyOfRange(middle, rootIndex + 1, middleLen);
int[] rightLast = Arrays.copyOfRange(last, rootIndex, lastLen - 1);
//用递归再次构建左子树和右子树
TreeNode left = buildTree2(leftMiddle, leftLast);
TreeNode right = buildTree2(rightMiddle, rightLast);
//将左右子树添加到根节点
root.left = left;
root.right = right;
return root;
}
public static void main(String[] args) {
//前序、中序测试
// int[] pre = {18, 20, 16, 29, 39, 8};
// int[] middle = {16, 20, 39, 8, 29, 18};
//
// TreeNode root = buildTree(pre, middle);
// preorder_Traversal(root);
//中序、后序测试
int[] middle = {16, 20, 18, 39, 29, 8};
int[] last = {16, 20, 39, 8, 29, 18};
TreeNode node = buildTree2(middle, last);
preorder_Traversal(node);
}
}