一、基本概念
斯特林数出现在许多组合枚举问题中.
第一类斯特林数 StirlingS1[n,m], 给出恰包含 m 个圈的 n 个元素 的排列数目. 斯特林数满足母函数关系 . 注意某些 的定义与 Mathematica 中的不同,差别在于因子 .
第二类斯特林数 StirlingS2[n,m]给出把 n 个可区分小球分配到m个不可区分的的盒子,且盒子没有空盒子的方法的数量. 它们满足关系 . 划分函数 PartitionsP[n]给出把整数 n 写为正整数的和,不考虑顺序的方法的数目. PartitionsQ[n]给出把整数 n 写为正整数的和,并且和中的整数是互不相同的 写法的数目
设S(p,k)是斯特林数
S(p,k)的一个组合学解释是:将p个物体划分成k个非空的不可辨别的(可以理解为盒子没有编号)集合的方法数。
S(p,k)的递推公式是:
S(p,k) = k*S(p-1,k) + S(p-1,k-1) ,1<= k <=p-1
边界条件:
S(p,p) = 1 ,p>=0
S(p,0) = 0 ,p>=1
递推关系的说明:考虑第p个物品,p可以单独构成一个非空集合,此时前p-1个物品构成k-1个非空的不可辨别的集合,方法数为S(p-1,k-1);也可以前p-1种物品构成k个非空的不可辨别的集合,第p个物品放入任意一个中,这样有k*S(p-1,k)种方法。
第一类斯特林数和第二类斯特林数有相同的初始条件,但递推关系不同。引用Brualdi《组合数学》里的一段注释“对于熟悉线性代数的读者,解释如下:具有(比如)实系数,最多为p次的那些各项式形成一个p+1维的向量空间。组1,n,n^2,...。n^p和组A(n, 0),A(n,1),A(n,2),... ,A(n,p)都是该空间的基。第一类Stirling数和第二类Stirling数告诉我们如何用其中的一组基表示另一组基。”
二、解释
第一类Siteling_Number
第一类Stirling数是有正负的,其绝对值是 个元素的项目分作
个元素的项目分作 个环排列的方法数目。常用的表示方法有
个环排列的方法数目。常用的表示方法有![s(n,k) , \left[\begin{matrix} n \\ k \end{matrix}\right]](http://upload.wikimedia.org/math/8/4/9/8494c8de074f7e71c7fbb634d3f83fd6.png) 。
。
换个较生活化的说法,就是有 个人分成
个人分成 组,每组内再按特定顺序围圈的分组方法的数目。例如
组,每组内再按特定顺序围圈的分组方法的数目。例如 :
:
- {A,B},{C,D}
- {A,C},{B,D}
- {A,D},{B,C}
- {A},{B,C,D}
- {A},{B,D,C}
- {B},{A,C,D}
- {B},{A,D,C}
- {C},{A,B,D}
- {C},{A,D,B}
- {D},{A,B,C}
- {D},{A,C,B}
这可以用有向图来表示。

给定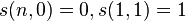 ,有递归关系
,有递归关系
递推关系的说明:考虑第n+1个物品,n+1可以单独构成一个非空循环排列,这样前n种物品构成k-1个非空循环排列,方法数为s(n,k-1);也可以前n种物品构成k个非空循环排列,而第n+1个物品插入第i个物品的左边,这有n*s(n,k)种方法。
 是调和数的推广。
是调和数的推广。
 是递降阶乘多项式的系数:
是递降阶乘多项式的系数:
性质
第二类Siteling_Number
第二类Stirling数是 个元素的集定义k个等价类的方法数目。常用的表示方法有
个元素的集定义k个等价类的方法数目。常用的表示方法有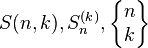 。
。
换个较生活化的说法,就是有 个人分成
个人分成 组的分组方法的数目。例如有甲、乙、丙、丁四人,若所有人分成1组,只有所有人在同一组这个方法,因此
组的分组方法的数目。例如有甲、乙、丙、丁四人,若所有人分成1组,只有所有人在同一组这个方法,因此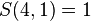 ;若所有人分成4组,只可以人人独立一组,因此
;若所有人分成4组,只可以人人独立一组,因此 ;若分成2组,可以是甲乙一组、丙丁一组,或甲丙一组、乙丁一组,或甲丁一组、乙丙一组,或其中三人同一组另一人独立一组,即是:
;若分成2组,可以是甲乙一组、丙丁一组,或甲丙一组、乙丁一组,或甲丁一组、乙丙一组,或其中三人同一组另一人独立一组,即是:
- {A,B},{C,D}
- {A,C},{B,D}
- {A,D},{B,C}
- {A},{B,C,D}
- {B},{A,C,D}
- {C},{A,B,D}
- {D},{A,B,C}
因此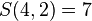 。
。
给定 ,有递归关系
,有递归关系
递推关系的说明:考虑第n个物品,n可以单独构成一个非空集合,此时前n-1个物品构成k-1个非空的不可辨别的集合, 方法数为S(n-1,k-1);也可以前n-1种物品构成k个非空的不可辨别的 集合,第n个物品放入任意一个中,这样有k*S(n-1,k)种方法。
 是二项式系数,B_n是贝尔数。
是二项式系数,B_n是贝尔数。
两者关系
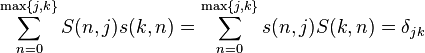
 是克罗内克尔δ。
是克罗内克尔δ。
三、例题
http://acm.hdu.edu.cn/showproblem.php?pid=3625
https://www.luogu.org/problemnew/show/P3904
四、参考文章
https://www.cnblogs.com/owenyu/p/6724661.html



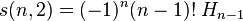
![s(n,3) = \frac{1}{2} (-1)^{n-1} (n-1)! [ (H_{n-1})^2 - H_{n-1}^{(2)} ]](http://upload.wikimedia.org/math/8/b/0/8b074a8e91fdb536ac2e87387cf3ff12.png)
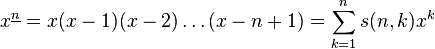












![[DiceCTF 2023] rSabin](https://img-blog.csdnimg.cn/img_convert/c400e93ddc68fd032a3e8aeb7c634327.png)
![[密码学复习]Cryptography](https://img-blog.csdnimg.cn/img_convert/63e15cb89a47b92f703c9bf12cf0cf10.png)


