目录

1.public static Vector3 Project(Vector3 vector, Vector3 onNormal);

描述  ：

代码：

效果：

结论：

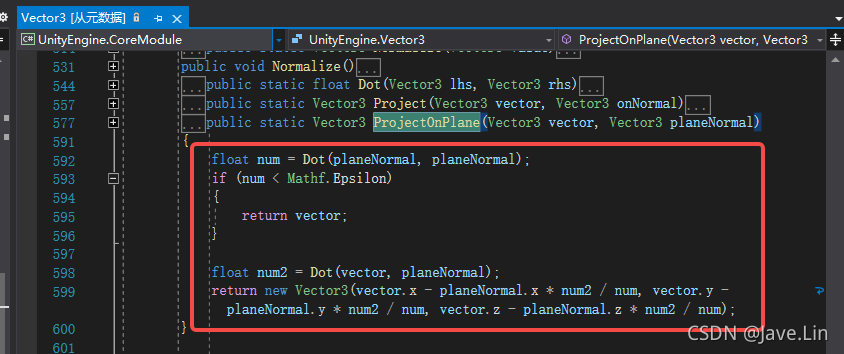
2.public static Vector3 ProjectOnPlane(Vector3 vector, Vector3 planeNormal);返回向量在平面上的位置。 

描述  :

代码：

效果：

 画出法向量平面代码：

效果：

结论：

---

1.public static Vector3 Project(Vector3 vector, Vector3 onNormal);

描述  ：

将一个向量投影到另一个向量上。  
为了理解矢量投影，假设onNormal位于指向其方向的直线上。 沿着这条线的某处是离矢量尖端最近的点。 投影只是在onNormal上缩放，使它到达直线上的那个点。
如果onNormal几乎为零，函数将返回零向量。 

代码：

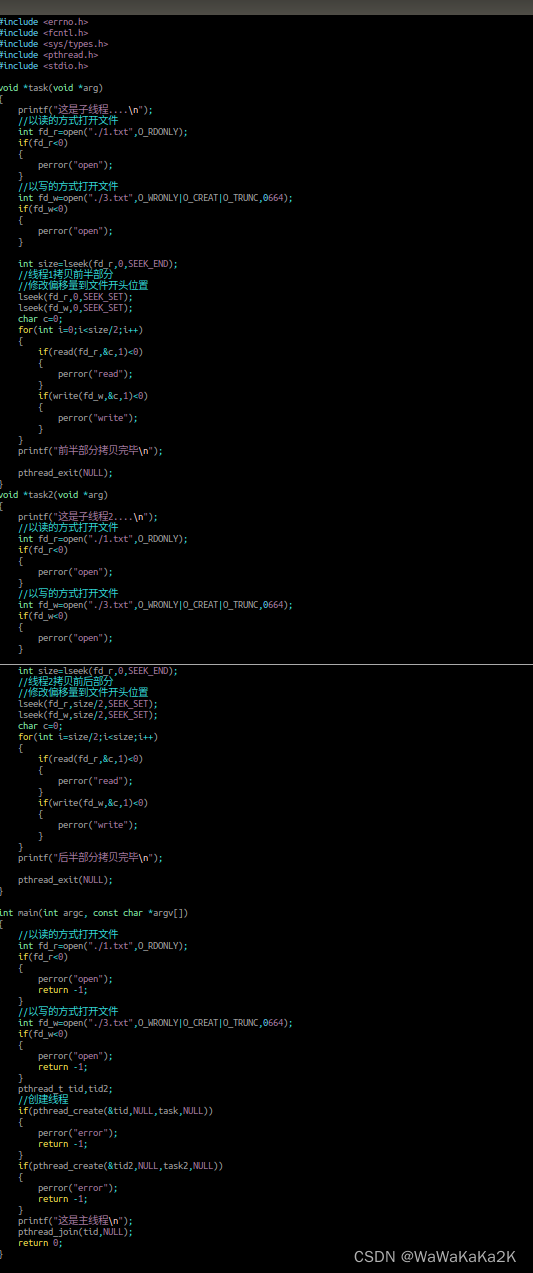
    public Transform A;public Transform B;Vector3 planX;Vector3 planY;Vector3 planZ;// Start is called before the first frame updatevoid Start() {//dir1 = new Vector3(0, 5, 5);}// Update is called once per framevoid Update() {Vector3 dir = A.position - B.position;Debug.DrawLine(B.position, A.position, Color.cyan);planX = Vector3.Project(dir, Vector3.left);planY = Vector3.Project(dir, Vector3.up);planZ = Vector3.Project(dir, Vector3.forward);Debug.DrawLine(B.position, B.position + planX, Color.white);Debug.DrawLine(B.position, B.position + planY, Color.black);Debug.DrawLine(B.position, B.position + planZ, Color.gray);}

效果：

结论：

白线是向量AB以B为起点在X轴上的投影
黑线是向量AB以B为起点在Y轴上的投影
灰线是向量AB以B为起点在Z轴上的投影

2.public static Vector3 ProjectOnPlane(Vector3 vector, Vector3 planeNormal);返回向量在平面上的位置。 

描述  :

将一个向量投影到一个由与该平面正交的法向量定义的平面上。 

代码：

我们尝试把一个向量与x轴的正方向传入此方法
即：

    public Transform A;public Transform B;Vector3 projectOnPlanX;// Start is called before the first frame updatevoid Start() {}// Update is called once per framevoid Update() {Vector3 dir = A.position - B.position;projectOnPlanX = Vector3.ProjectOnPlane(dir, Vector3.left);Debug.DrawLine(B.position, B.position + projectOnPlanX, Color.red);}

效果：

红线就是这个方法返回的向量+向量B

根据定义我们可以知道 红线是 向量A - 向量B 在 我们传入的X轴正交的法向量平面上 然后我们画出这个平面

 画出法向量平面代码：

 public Transform A;public Transform B;Vector3 projectOnPlanX;Vector3 dir1;// Start is called before the first frame updatevoid Start() {dir1 = new Vector3(0, 20, 20);}// Update is called once per framevoid Update() {Vector3 dir = A.position - B.position;dir1 = Quaternion.AngleAxis(2, Vector3.left) * dir1;Debug.DrawRay(B.position, dir1, Color.green, 7f);}

效果：

由绿色射线组成的平面即是与我们传入的x轴正交的法向量平面（严格来说我们画出的应该是重合于这个平面的圆）

由此可以看出 图一中的红色射线投影到了我们所画的平面上

如下图：

由此我们可以得出：
Vector3 plane = Vector3.ProjectOnPlane(向量A-向量B, Vector3.left);

向量plane的模就是 向量A 和 向量B 在YZ轴组成的坐标系中的距离

如果我们这样
Vector3 plane = Vector3.ProjectOnPlane(向量A-向量B, Vector3.up);
向量plane的模就是 向量A 和 向量B 的地面距离

结论：

Vector3.ProjectOnPlane(Vector3 vector,Vector3 onNormal ) 得到的是

向量vector      在    向量onNormal的垂直平面上的投影向量