解决的问题：

梯度消失，深层网络难训练。

• 因为梯度反向传播到前面的层，重复相乘可能使梯度无穷小。结果就是，随着网络的层数更深，其性能趋于饱和，甚至迅速下降。

关于为什么残差结构（即多了一条跳跃连接线后）为什么一定程度缓解了梯度消散的数学推导：

核心思想：

1. 引入一个恒等快捷键（也称之为跳跃连接线），直接跳过一个或者多个层。
   
   当有这条跳跃连接线时，网络层次很深导致梯度消失时，$F(x)=0，y=g(0+x)=relu(x)=x$

• 在网络上堆叠这样的结构，就算梯度消失，我什么也学不到，我至少把原来的样子恒等映射了过去，相当于在浅层网络上堆叠了“复制层”，这样至少不会比浅层网络差。

• 万一我不小心学到了什么，那就赚大了，由于我经常恒等映射，所以我学习到东西的概率很大。

2. 当尺寸一样时才可以相加 “⊕” ，当尺寸不一样时，需要调成一样的再相加 “⊕” ，如下所示。

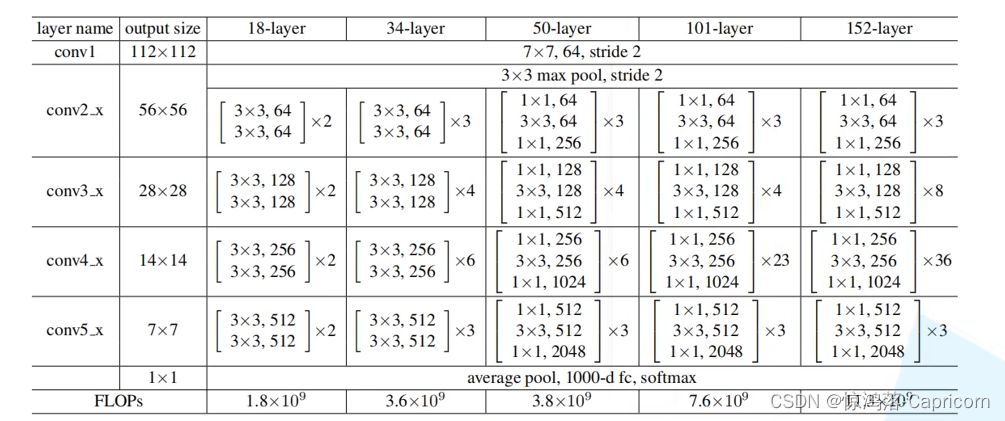
3. 而所谓Resnet-18，Resnet-50等，不过是层数不一罢了，如下图，惯用的是Resnet-50与Resnet-101。
   

总结

1. ResNet的残差连接使得模型的深度似乎不再是限制，具体的原因可能是在堆叠的非线性映射中，神经网络难以学习到一个恒等映射，而残差连接使之更容易。
2. 还有观点认为残差连接打破了神经网络的对称性，提高了每层神经元的利用率，另外网络能够加深也可能是因为多条支路保证了即使某些层退化也不会影响整体表现。