统计学上的因素是指研究者关心的实验条件，而水平是指因素的具体表现形式。

6.1 单因素方差分析

6.1.1 原理

单因素方差分析仅研究了单个研究因素，该因素有多个水平（≥3，如果为2个水平就用T检验了），方差分析就是通过分析处理组均数之间的差别，推断试验所代表的多个总体均数间是否存在差别。

其原理是将全部观察数据的变异（总变异）分解为组间变异和组内变异，如果组间的变异远远大于组内变异，则有理由认为本次研究的因素发挥着作用。

（1）总变异：每个实验对象数据与总体均数的差异；

（2）组间变异：各处理组的样本均值与总体均数的差异；

（3）组内变异：各处理组内部观察值与该组均数的差异。

三者之间的关系：总差异=组间差异+组内差异

当组间差异和组内差异均只反映随机误差，即各样本来自同一总体，各组均数之间无差别；当各样本不是来自同一总体，组间差异反映处理效应和随机误差，而组内变异只反映随机误差，即组间变异大于组内变异，具体可用F检验来进行。

理论上当F值大于1时，认为处理因素有作用，即存在处理效应；当F值等于1时，可认为处理因素无作用或处理效应不显著，各组样本均值差异可以由随机误差来解释。

6.1.2 操作步骤

（1）单因素方差分析

单击“分析”-“比较平均值”-“单因素ANOVA”，弹出“单因素方差分析”对话框如下：

（2）单击“对比”按钮，弹出如下对话框：

 

多项式：选择是否对方差分析的组间平方和进行分解并进行趋势检验；

度：选中“多项式”后，此下拉菜单被激活，用于选择进行趋势检验的曲线类型，包括线性、二次项、三次、四次项和五次项；

第1/1项对比：用于精确定义组间均值比较的多项式系数。一般按照分组变量升序给每组一个系数值，但务必要保证所有系数和为零。列表中的第一个系数对应于分类变量的最小值，最后一个系数对应于分类变量的最大值。可以同时建立多个多项式，一个多项式的一组系数输入结束后，单击“下一张”按钮，输入下一组数据。

（3）单击“事后比较”按钮，弹出如下对话框：

①假定等方差：包括14中两两比较的方法

LSD法:最小显著性差异法，用T检验完成组间成对均值的比较，检验的敏感度较高，即使各个水平间的均值存在细微差别也能被检验出来，但此法对第I类弃真错误不进行控制和调整；

Bonferroni法：为修正最小显著性差异法，用T检验完成组间成对均值的比较，即通过设置每个检验的误差率来控制整个误差率，采用此法看到的显著值是多重比较完成后的调整值；

Sidak法：用T检验统计量完成多重配对比较后，为多重比较调整显著值，其比Bonferroni法的界限要小。

等等...

②不假定等方差：包括四种两两比较的方法

Tamhane's T2法：表示采用T检验的保守成对比较；

Dunnett's T3法：指用学生化最大系数进行配对比较检验；

Games-Howell 法：表示执行方差不齐时的配对比较检验，该方法比较常用；

Dunnett'S C 法：表示用Student-Range 极差统计量进行配对比较检验。

③“显著性水平”为本次检验的检验水准，通常设置为0.05。

（4）单击“选项”按钮，弹出如下窗口：

 

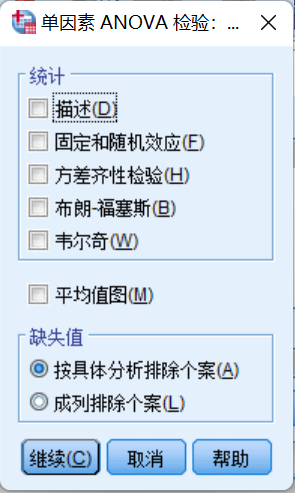
①统计栏：
描述：选中该项，则结果中输出每个因变量的个案数、均值、标准差、均值的标准误、最小值、最大值和均值的95%可信区间；

固定和随机效应：表示显示固定效应模型的标准差、标准误和95%置信区间以及显示随机效应模型的标准误、95%置信区间、方差成分间的估计值；

方差同质性检验：选中此项，计算Levene方差齐性检验；

Brown-Forsythe :表示计算分组均值相等的Brown-Forsythe 统计量。当方差齐性未知时，此检验比F统计量更有优势；

Welch：与Brown-Forsythe类似，当不能把握方差齐性时，比F检验稳健。

②均值图：输出各组的均值图，可以辅助判断各组间的趋势。

③缺失值：选择处理缺失值的方式。“按具体分析排除个案”表示在分析时，检验变量中含有缺失值的将不被计算；“成列排除个案”表示任何一个变量中含有缺失值的个案都将不被计算。

（5）自助抽样

主要功能为让计算机对研究样本进行反复抽样，根据多次抽样的结果对总体均数的置信区间进行估计。单击“自助抽样”按钮，弹出如下对话框：

 ①执行自助抽样：选择此项，其他复选框将被激活，建议样本数不低于1000;

②设置梅森旋转算法种子：选择此项，是为了让分析结果能够复制，即再运行时，设置同样的种子数，会得到相同的结果。

③置信区间：级别通常被设定为95%，有两种方法：“百分位数”，其95%置信区间值P2.5~P97.5；“加速纠正偏差”法，是对百分位数法的修正，结果更为精确，也需要更多的时间进行计算。

④“抽样”栏指定系统进行反复抽样具体采用的方法

简单：指系统从原始资料中不断抽取样本计算统计量后放回；

分层：是按照原始资料某个特征进行分层，然后再进行抽样。但层内单位同质性较高，而层之间单位差异较大时，分层法抽样更为科学。

6.1.3 实例详解

例：比较三个不同电池生产企业生产电池的寿命，此例企业为因素，不同厂家为水平。

（1）单击“分析”-“比较平均值”-“单因素ANOVA”，弹出如下对话框：

（2）单击“对比”按钮，弹出如下对话框：

 

单击“继续”，返回主对话框。

（3）单击“事后比较”按钮，弹出如下对话框，本例选择LSD法和Tamhane's T2法进行讲解。

 

 （4）单击“选择”按钮，弹出如下对话框，选择“描述”、“方差齐性检验”和“平均值图”

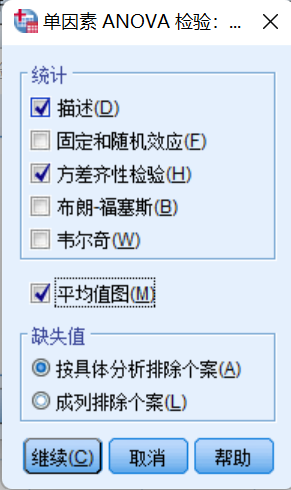
单击“继续”返回对话框。

（5）单击“确定”按钮运行，输出结果如下：

 上图为描述性统计量的结果，分别列出了三个企业的样本量、均值、标准偏差等。

 上图为Levene方差齐性检验的结果，本例莱文统计量为0.039，显著性P值=0.680>0.05，故三组数据方差齐性。

 上图为单因素方差分析的结果，并进行了趋势检验，结果显示不同企业间方差分析统计量F=38.771，P值=0.000<0.01，因此认为不同企业间生产电池的寿命不同。

 上图为事后比较的结果，分别为LSD法和Tamhane法，显著性小于0.05表示有差异。本例应该看LSD的结果，因为前面莱文方差齐性检验显示方差齐性。

上图为均值图，对不同电池生产企业电池寿命的均值进行作图，可形象展示各组均值间的差异，图中可见企业2与企业1和3相差较大，结果与LSD法结果相同。