个人总结 - JS逆向解析

目前加密的方式总结有下面几点：

对称加密（加密解密密钥相同）：DES、DES3、AES
非对称加密（分公钥私钥）：RSA
信息摘要算法/签名算法：MD5、HMAC、SHA
前端实际使用中MD5、AES、RSA，自定义加密函数使用频率是最高的
几种加密方式配合次序：采用非对称加密算法管理对称算法的密钥，然后用对称加密算法加密数据，用签名算法生成非对称加密的摘要
DES、DES3、AES、RSA、MD5、SHA、HMAC传入的消息或者密钥都是bytes数据类型，不是bytes数据类型的需要先转换；密钥一般是8的倍数
Python实现RSA中，在rsa库中带有生成签名和校对签名的方法
安全性：DES<DES3=AES<RSA,至于MD5、SHA、HMAC不好说了

搜其他关键词如RSA、encrypt，尤其是encrypt

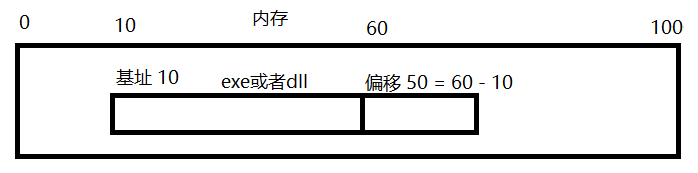
其中this.exponent是RSA加密偏移量，数值一般在HTML文件里面，全局搜索，其value值就是

密钥的值一般在网页源码的一个元素值。全局搜索，其value值就是，或者是js中找到

AES：案例ewt360.com

AES是典型的对称加密，密钥就在前端源码里，相对于非对称的RSA安全性很低

var com_str = {_KEY: "20171109124536982017110912453698",//32位_IV: "2017110912453698",//16位*str：需要加密的字符串Encrypt: function (str) {var key = CryptoJS.enc.Utf8.parse(this._KEY);var iv = CryptoJS.enc.Utf8.parse(this._IV);var encrypted = '';var srcs = CryptoJS.enc.Utf8.parse(str);encrypted = CryptoJS.AES.encrypt(srcs, key, {iv: iv,mode: CryptoJS.mode.CBC,padding: CryptoJS.pad.Pkcs7});return encrypted.ciphertext.toString();},}

此处还调用了CryptoJS，它是加密的核心类，但发现没有，其实是藏在另外一个js文件中，找到并复制出来，将两个js合并即可

自定义加密：空中网

这个网站是以get方式登陆的，由一个eval加密的js

function encrypt （）
this.encrypt(pwd, this.j_data["dc"])加密原理：在打开网站的时候服务器会返回一串字符串，用于加密，加密的js是通过eval方式处理的

js混淆：就是把其中的变量、方法位置顺序打乱，但是又用一些无关的变量或者方法来保证执行顺序

解决方法：复制完整的混淆代码去js混淆还原网站还原。

注意：很多时候，js代码的生成函数都进行了伪装，核心的东西只有一句，但有一堆混淆视听的js，只需要找到核心代码，进行解析就行

eval加密：

eval()方法：js中的eval()方法就是一个js语言的执行器，它能把其中的参数按照JavaScript语法进行解析并执行，简单来说就是把原本的js代码变成了eval的参数，变成参数后代码就成了字符串，其中的一些字符就会被按照特定格式“编码” 。

例如下：

eval(function(p,a,c,k,e,d){e=function(c)
{return(c<a?'':e(parseInt(c/a)))+((c=c%a)>35?
String.fromCharCode(c+29):c.toString(36))};
if(!''.replace(/^/,String)){while(c--)d[e(c)]=k[c]||e(c);k=[function(e){return 
d[e]}];e=function(){return'\\w+'};c=1};while(c--)if(k[c])p=p.replace(new 
RegExp('\\b'+e(c)+'\\b','g'),k[c]);return p}('5 4="粘贴要加密/解密的3代码到这里";2(0==0){  
1(4);}',62,6,'1|alert|if|javascript|showmsg|var'.split('|'),0,{}))

解决方法：将代码字符串放入javascript Eval官网解密

再看eval解密后的js文件尾部，有下面一个函数

function encryptString(str, e, m) {var key = RSAUtils.getKeyPair(e, '', m);return RSAUtils.encryptedString(key, str)
}

发现是RSA加密方式，那现在从RSA加密逆向搜索encryptString关键词，找到下面

var timesign = (new Date).getTime() + timespan;$("#p1User").val(encryptString(timesign + encodeURIComponent($("#passwordUser").val()), $("#rsaExponent").val(), $("#rsaModulus").val()));$("#password_value").val($("#passwordUser").val());$("#btnSubmitUser").val("登录中...");$("#usernameUser").addClass("fontcolor_cccUser").attr("readonly", "readonly");$("#passwordUser").val("").addClass("fontcolor_cccUser").attr("readonly", "readonly");

筛选核心代码

encryptString(timesign + encodeURIComponent($("#passwordUser").val()),$("#rsaExponent").val(), $("#rsaModulus").val());

("#passwordUser").val()，rsaExponent").val(), $("#rsaModulus").val()

这三个参数分别是从页面获取id，去html搜索这三个关键词

rsaExponent 看到value为01001，故此RSA加密偏移量为01001

rsaModulus 也是看到value为一群乱码，它是RSA密钥

用户认证的话会涉及到cookie

解决方法：查看cookie数据，找到经过例如：fingerprint进行URL解码，对比请求参数fingerprint修改

那么，逆向解密解决思路呢？

逆向解密解决思路:

（1）是根据加密参数，如“x-uab”关键字在所有关键中查找

打开chrome浏览器按F12
找到点击source中按ctrl + shift + F快捷键，输入x-uab找到js代码
接下来，打个断点调试一下：在数字那里点一下，数字位置出现蓝点，表示添加断点成功
然后刷新获取店铺列表的页面，程序会在断点处停下，在控制台调试o.getUA()函数，看一下输出
继续向下查看这个关键词参数 js 生成函数的引用，一步步往回推，找到最原始的 js 生成方法
找到以后，把这个function 方法全部代码取出来，另存为一个js文件。

（2）怎么用python执行js脚本？

方法一：

自己搞懂生成的过程，是md5还是AES加密，找到key值，时间戳其余参数啥的也可以生成，做过后台开发的会比较清楚其生成原理，因为需要对接前后端接口

方法二：execjs

因为在上面复制出来的脚本中，只单单定义了一个方法，并没有调用这个方法，所以，要在js文件的末尾添加一些代码来调用

function getParam() {var a;var param = e(2,a);return param
};

然后，开始撸Python代码吧

原理：将execjs的引擎换成PhantomJS这个无头浏览器，换句话说就是用PhantomJS来执行js脚本，PhantomJS是一个浏览器，自然就会创建window对象。

import execjsimport os
os.environ["EXECJS_RUNTIME"] = "PhantomJS"
node = execjs.get()
file = 'eleme.js'
ctx = node.compile(open(file).read())
js_encode = 'getParam()'
params = ctx.eval(js_encode)
print(params)

不用PhantomJS方法

import execjsnode = execjs.get()
file = 'eleme.js'
ctx = node.compile(open(file).read())
js_encode = 'getParam()'
params = ctx.eval(js_encode)
print(params)可能会报错：execjs._exceptions.ProgramError: TypeError: 'window' 未定义
原因：window对象估计是浏览器打开是创建的，蕴含浏览器的信息，所以用Python来执行这段代码时，没有这个对象

方法三：

思路和方案二类似，不过更加粗暴一些。因为没在浏览器执行，那就模拟浏览器来执行。

在执行之前，同样要修改js脚本，在js文件末尾调用e方法，添加如下代码，例：

var a;
var param = e(2,a);
return param;

注意：调用方法不要放在任何函数里面，我之前就是因为将这段代码放在函数里头强制执行，导致的结果就是在浏览器里可以获取加密字符串，但是在Python中获取到的却是None

模拟浏览器用的selenium和chrome的webDriver，代码如下：

from selenium import webdriverbrowser = webdriver.Chrome(executable_path='chromedriver.exe')
with open('eleme.js', 'r') as f:js = f.read()
print(browser.execute_script(js))

最终获得加密之后的字符串

最后，有必要说一下，如果需要获取大量的x-uab，采用方案三效率会高一下，因为采用方案二的话，可以自打开一个浏览器（都调用一个webdriver对象），然后快速执行js，返回加密字符串。