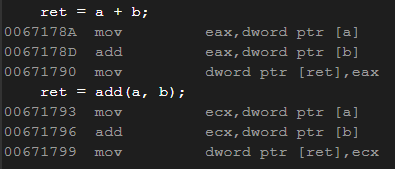
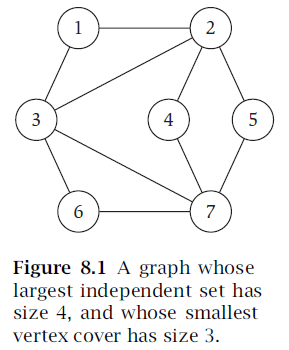
Logit Adjust

BER

我们在分类问题中常用的误分类函数使得分类器最终学到的分布：
$\propto P(y)P(x|y)$
假设在一个不平衡猫狗二分类问题中，狗是一个小类，只有整个数据集的1%的数据量。则 $P (y) = 0.01$ ，这样无论 $P (x ∣ y)$ 有多大，右边这一项都会很小。所以作者使用BER即banlance error rate，

首先举一个例子方便快速理解BER的思想：
源地址
在这里插入图片描述

根据上面这个混淆矩阵有 $(\frac{b}{a+b}+\frac{c}{c+d})$ 通常的误差计算公式则为 $ER=\frac{b + c}{a+b+c+d}$ 再看原文中给出的BER的公式：
$\frac{1}{L}\sum_{y \in [L]}P_{x|y} (y \notin argmax_{y^{\prime} \in \hat{y}}f_{y^{\prime}}(x))$
$\hat{y}$ 等价于原文中的花体y,有 $\hat{y}=[L]={1, 2, \dots L}.$ 上式右边用人话翻译过来就是“把所有（类别） $y$ 被分类器 $f_{y^\prime}(x)$ 误分类的概率加起来，最后对类别数做平均”。精髓就在于误差的计算是class-wise的，想想我们通常评估误差率，都是用一个batch中，用 $\frac{误分类样本数}{batchsize}$ 来表示，这个时候分类器就可以偷懒，只要把所有样本都预测为大类就可以在误差率这个评价指标上表现良好。一个问题在于，为甚么上式积分符号下面有一个” $x ∣ y$ ”，这个条件函数的假设是怎么回事？ 在我的理解中x是样本，再结合最开始举得例子， $\frac{b}{a+b}$ 左边翻译过来是“已知为类别y，则其为样本x的概率”，右边翻译过来是“类别y的准确率”，这两者要怎么画上等号呢？还请读者不吝赐教。
BER鼓励分类器学到的分布：
$\propto \frac{1}{L}P(x|y)$
这样分类器分类时就不会再受到不平衡数据集的影响。但是考虑另一个问题，如果狗这个小类中全部都是二哈，只有一个泰迪，那么分类器很可能会学到 $\to 1$ ，这相当于一个不平衡子集的问题。

Logit Adjustment

最小化BER可以表述为 $f^* \in argmin_{f:x \to R^{L}}BER(f)$ ,原文提到这个问题的一个典型的解是：“the best posible or Bayes-optimal score as following:”
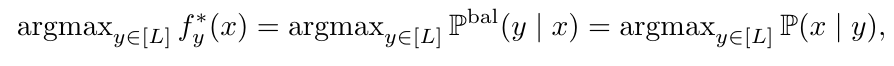
在这里插入图片描述
上式右边的等式与上一节中分析BER鼓励分类器学习的分布的形式是一致的。文章中进一步阐述，当类别条件概率 $P (x ∣ y ）$ 固定的时候，无论 $P (y)$ 怎么变，模型都是无视的，这就直观的解释了，为什么BER可以用于解决类别不平衡的问题。
　　接着作者假设 $\propto exp(s^*_y(x))$ ，其中 $s^*:x \to R^L$ 是一个记分器（scorer），用来把样本x映射为一个长度为L向量，向量中的每个元素表示分类器认为该样本属于某一类的分数。使用指数函数一是因为它本身是 $R^n$ 上单调增的二是因为在外面套上对数函数之后可以把它消掉。同时根据定义有 $P^{bal}(y|x) \propto P(y|x)/p(y)$ 。因此上面的长等式又可以表示为：
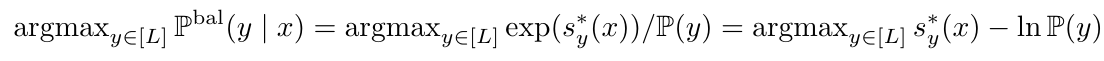在这里插入图片描述上式最后一项就是作者所谓的logit adjust。作者提出可以有两种形式来执行，其一是整合在loss函数中，其二是在测试的时候做后处理。第一种方式定义的损失函数如下：

def build_loss_fn(use_la_loss:bool, base_probs, tau=1.0):def loss_fn(logits, labels):if use_la_loss:logits = logits + torch.log(torch.tensor(base_probs**tau + 1e-12,dtype=torch.float32,device="cuda",).detach())loss = F.cross_entropy(logits, labels)return lossreturn loss_fn

tau默认是1，也就是不起任何作用，作者给的推荐配置中也没有对这个参数进行修改。加1e-12应该是为了数值稳定性。
　　最后作者认为自己的方法相对于之前的方法的优势之一是有坚实的统计学基础：最小化平衡误差时保证了费雪一致性（Fisher consistent）。关于这个性质我的浅薄理解就是在一个采样上{X}求得的函数 $\to \theta$ ,对于真实分布仍然适用。用人话来说就是，我这个函数可以根据这个采样求得这个分布的一个未知参数 $\theta$ ，把这个函数放到真实分布上仍然是正确的，这样我求的这个函数就可以以偏概全。