1.虚拟变量

直接在回归模型中加入定性因素（比如类别因素：男或女）存在困难，因此可以考虑把定性因素量化，使定性因素与定量因素在回归模型中起到相同的作用。这时就用到了虚拟变量。

计量经济学中，把取值为0或者1的变量称为虚拟变量。例如用0表示女、1表示男。这样就把定性因素进行了量化。

2.虚拟变量陷阱

对于定性因素性别而言，它有两个水平——男和女，可以用一个虚拟变量x表示，x=1表示男，x=0表示女；也可以用两个虚拟变量x和y表示，x=1表示是男，x=0表示不是男，同理y=1表示女，y=0表示不是女。

若定性因素有m个互相排斥的属性（例如定性因素“性别”有m=2个相互排斥的属性——男和女）：
（1）当回归模型有截距项时，只能引入m-1个虚拟变量，否则就会陷入“虚拟变量陷阱”；
（2）当回归模型无截距项时，可以引入m个虚拟变量。

3.虚拟变量陷阱例子及分析

下述例子中y是因变量，自变量有C1、C2、C3。

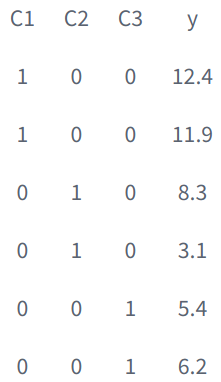
在有截距项b时，回归模型为
　　　　　　　　　　　　　　　y=a1×C1+a2×C2+a3×C3+b。
按上图中的虚拟变量设置，用OLS（ordinary least squares）求解方程的时候，模型解为
　　　　　　　　　　　　　　　[a1,a2,a3,b]’=invert((X’X))X’Y，
当有截距项b的并用时候，用上述公式求解模型就会遇到“虚拟变量陷阱”。

用上述公式求解回归模型的R语言代码如下：

##实验1：有截距项b+3个虚拟变量  【本实验报错】
##dv.csv为上述的表格
dv=read.csv('dv.csv')
Y=dv$y
X=cbind(dv[,c(1,2,3)],b=rep(1,6))
X=matrix(unlist(X),nrow=6)
solve(t(X)%*%X)

实验1报错，报错信息为:Error in solve.default(t(X)%*%X):Lapack例行程序dgesv:系统正好是奇异的:U[4,4]=0。

上述实验说明矩阵X’X是不可逆的。此时，有两种办法避免“虚拟变量陷阱”：去掉截距项b或者减少一个虚拟变量，改进代码如下：

##实验2：减少第一个虚拟变量
Y=dv$y
X=cbind(dv[,c(2,3)],b=rep(1,6))
X=matrix(unlist(X),nrow=6)
solve(t(X)%*%X)%*%t(X)%*%Y##实验3：去掉截距项b
Y=dv$y
X=cbind(dv[,c(1,2,3)])
X=matrix(unlist(X),nrow=6)
solve(t(X)%*%X)%*%t(X)%*%Y

上述两种方法都计算成功，当然系数是不一样。

4.总结

可以看到所谓“虚拟变量陷阱”的原因是：多重共线性导致OLS算法中矩阵不可逆。从而无法计算回归模型的系数。

“虚拟变量陷阱”是和回归模型的求解算法有关的，上述的OLS的闭式解会报错，但是可能用其他求解算法（比如梯度下降）还可以计算。

上述数据如果用Python的 sklearn.linear_model.LinearRegression（默认是有截距项b的），X={C1,C2,C3}，Y={y}，是不会报错的。但是用R中的线性回归函数lm时（参数也是X={C1,C2,C3}，Y={y}）计算出的一个系数是NA。用python解出的回归模型和用上述实验3计算出的模型实际结果几乎一样———6个数据点上的误差都是0或者8.881784e-16。二者对比代码如下：

import pandas as pd
from sklearn.linear_model import LinearRegressiondv=pd.read_csv('dv.csv')lr=LinearRegression()
lr.fit(X=dv.iloc[:,[0,1,2]],y=dv.iloc[:,3])
#sklearn———LinearRegression回归模型误差
error1=lr.coef_[0]*dv.iloc[:,0]+lr.coef_[1]*dv.iloc[:,1]+lr.coef_[2]*dv.iloc[:,2]+lr.intercept_-dv.iloc[:,3]
#上述实验3 回归模型误差，系数是从R计算结果copy过来的
error2=12.15*dv.iloc[:,0]+8.20*dv.iloc[:,1]+5.80*dv.iloc[:,2]-dv.iloc[:,3]
print(error1-error2)

5.参考资料

（1）本文的例子从下面这个资料里选的。这个资料讲的更清楚：
既有解释又有例子的一个文档
（2）这个ppt不错，前12页是解释虚拟变量的：
百度文库解释虚拟变量回归的一个文档