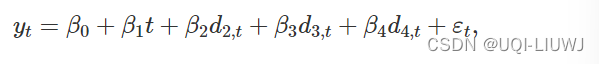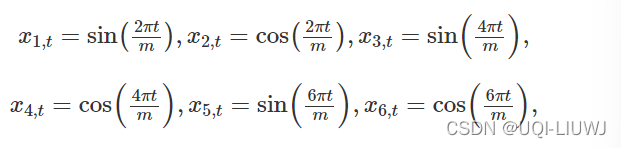1 前言
- 当预测变量是分类变量时,我们可以引入虚拟变量,作为回归的虚拟变量
- 虚拟变量也可用于解释数据中的异常值。 虚拟变量不会忽略异常值,而是消除其影响。 在这种情况下,虚拟变量对该观察值取值为 1,而在其他任何正常的地方取值为 0。
2 季节性虚拟变量
假设我们正在预测每日数据,并且我们希望将星期几作为预测变量。 然后可以创建以下虚拟变量。
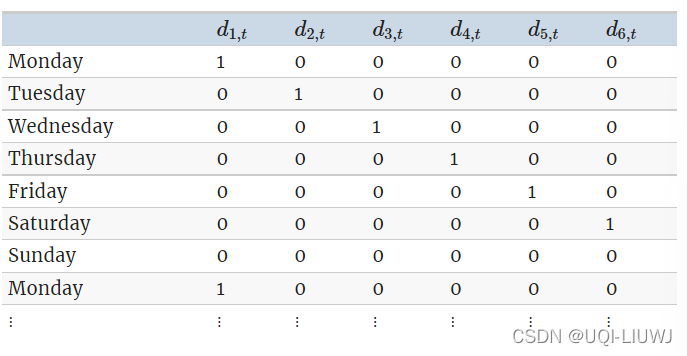
请注意,对七个类别进行编码只需要六个虚拟变量。 这是因为第七类(在本例中为星期日)被截距捕获,并在虚拟变量全部设置为零时指定。
与虚拟变量相关的每个系数的解释是,它是该类别相对于省略类别的影响的度量。 在上面的示例中,与星期一相关的 d1,t 系数将衡量星期一对预测变量的影响与星期日的影响相比。
2.1 举例
下面是一个解释虚拟变量系数含义的示例,该系数反映了澳大利亚啤酒生产的季度季节性。
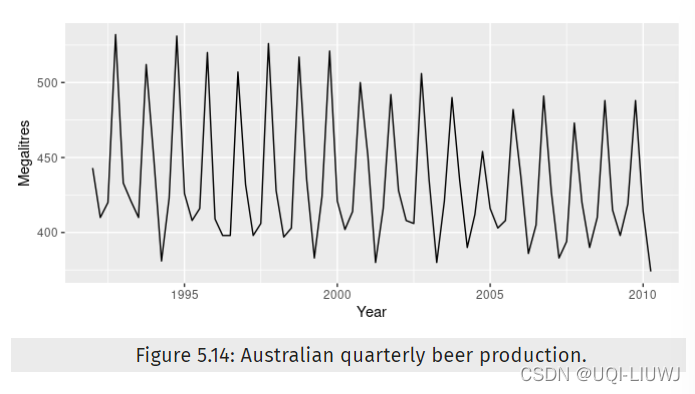
我们想预测未来啤酒生产的价值。 我们可以使用具有线性趋势和季度虚拟变量的回归模型对这些数据进行建模
如果 t 在第 i 季度,则 di,t=1,否则为 0。 第一季度变量已被省略,因此与其他季度相关的系数是衡量这些季度与第一季度之间差异的指标。
通过拟合,我们得到系数:
| β0 | 441.8 |
| β1 | -0.34 |
| β2 | -34.66 |
| β3 | -17.82 |
| β4 | 72.80 |
每季度平均下降趋势为 -0.34 兆升。 平均而言,第二季度的产量比第一季度低 34.7 兆升,第三季度的产量比第一季度低 17.8 兆升,第四季度的产量比第一季度高 72.8 兆升。
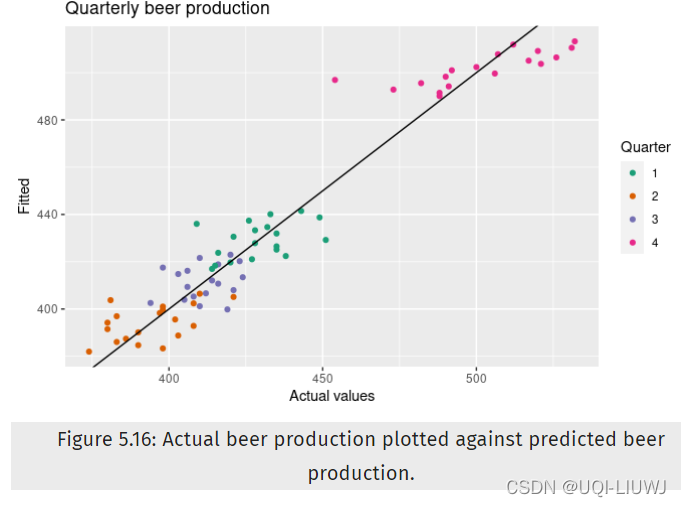
3 虚拟变量陷阱
许多人会尝试为第七类添加第七个虚拟变量。 这被称为“虚拟变量陷阱”,因为它会导致回归失败。 当还包括截距时,将有太多参数无法估计。
一般规则是使用的虚拟变量比类别少一个。 所以对于季度数据,使用三个虚拟变量; 对于月度数据,使用 11 个虚拟变量; 对于星期数据,使用六个虚拟变量,依此类推。
4 干预变量 Intervention variables
通常有必要对可能影响要预测的变量的干预措施进行建模。例如,竞争对手的活动、广告支出、行业行动等都会产生影响。
当效果只持续一个时期时,我们使用“尖峰”变量。这是一个虚拟变量,在干预期间取值为 1,在其他地方取值为 0。尖峰变量等效于用于处理异常值的虚拟变量。
其他干预措施具有即时和永久的效果,那么我们使用“步长”变量。阶跃变量在干预之前取值为零,从干预开始时取值为 1。
5 傅里叶级数
使用季节性虚拟变量的替代方法,特别是对于长季节性周期,是使用傅立叶项。
如果 m 是季节性周期,则前几个傅立叶项由下式给出
如果我们有每月的季节性,并且我们使用这些预测变量中的前 11 个,那么我们将得到与使用 11 个虚拟变量完全相同的预测。
使用傅立叶项,我们通常需要比虚拟变量更少的预测变量,尤其是当 m 很大时。 对于较短的季节性周期(例如季度数据),使用傅立叶项相对于季节性虚拟变量几乎没有优势。
包含傅立叶项的回归模型通常称为谐波回归,因为连续的傅立叶项表示前两个傅立叶项的谐波。
6 R语言实现
6.1 naive 线性回归
library(forecast)y<-ts(c(5,3,3.1,3.2,3.3,3.4,3.5,3.3,3.2,4,4.1,4.2,6,4,4.1,4.2,4.3,4.4,4.5,4.6,4.7,4.8,4.9,5,10,9,8,8.5,8.4,8.5,8.6,8.7,8.8,8.9,9,9.5),start = 2020,frequency = 12)x<-tslm(y~y)summary(x)#Call:
#tslm(formula = y ~ y)#Residuals:
# Min 1Q Median 3Q Max
#-2.686 -1.686 -1.036 2.814 4.314 #Coefficients:
# Estimate Std. Error t value
#(Intercept) 5.686 0.392 14.5
# Pr(>|t|)
#(Intercept) 2.28e-16 ***
#---
#Signif. codes:
#0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1#Residual standard error: 2.352 on 35 degrees of freedom
6.2 季节性虚拟变量
x<-tslm(y~y+season)#Call:
#tslm(formula = y ~ y + season)#Residuals:
# Min 1Q Median 3Q Max
#-2.367 -1.975 -1.033 3.000 3.667 #Coefficients:
# Estimate Std. Error t value
#(Intercept) 7.0000 1.6004 4.374
#season2 -1.6667 2.2633 -0.736
#season3 -1.9333 2.2633 -0.854
#season4 -1.7000 2.2633 -0.751
#season5 -1.6667 2.2633 -0.736
#season6 -1.5667 2.2633 -0.692
#season7 -1.4667 2.2633 -0.648
#season8 -1.4667 2.2633 -0.648
#season9 -1.4333 2.2633 -0.633
#season10 -1.1000 2.2633 -0.486
#season11 -1.0000 2.2633 -0.442
#season12 -0.7667 2.2633 -0.339
# Pr(>|t|)
#(Intercept) 0.000204 ***
#season2 0.468635
#season3 0.401438
#season4 0.459888
#season5 0.468635
#season6 0.495455
#season7 0.523126
#season8 0.523126
#season9 0.532534
#season10 0.631366
#season11 0.662568
#season12 0.737754
#---
#Signif. codes:
#0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1#Residual standard error: 2.772 on 24 degrees of freedom
#Multiple R-squared: 0.04766, Adjusted R-squared: -0.3888
#F-statistic: 0.1092 on 11 and 24 DF, p-value: 0.99976.3 傅里叶虚拟变量
x<-tslm(y~y+fourier(y,K=2))#Call:
#tslm(formula = y ~ y + fourier(y, K = 2))#Residuals:
# Min 1Q Median 3Q Max
#-2.756 -1.889 -1.040 2.972 3.700 #Coefficients:
# Estimate Std. Error
#(Intercept) 5.6861 0.4095
#fourier(y, K = 2)S1-12 -0.1321 0.5791
#fourier(y, K = 2)C1-12 0.4746 0.5791
#fourier(y, K = 2)S2-12 0.1251 0.5791
#fourier(y, K = 2)C2-12 0.3222 0.5791
# t value Pr(>|t|)
#(Intercept) 13.886 7.51e-15 ***
#fourier(y, K = 2)S1-12 -0.228 0.821
#fourier(y, K = 2)C1-12 0.820 0.419
#fourier(y, K = 2)S2-12 0.216 0.830
#fourier(y, K = 2)C2-12 0.556 0.582
#---
#Signif. codes:
#0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1#Residual standard error: 2.457 on 31 degrees of freedom
#Multiple R-squared: 0.03367, Adjusted R-squared: -0.09102
#F-statistic: 0.27 on 4 and 31 DF, p-value: 0.895Fourier() 的第一个参数允许它识别季节性周期 m 和要返回的预测变量的长度。 第二个参数 K 指定要包含多少对 sin 和 cos 项。 允许的最大值为 K = m / 2,其中 m 是季节性周期。