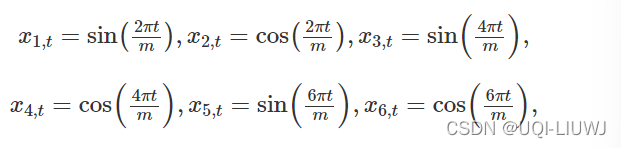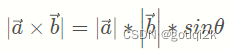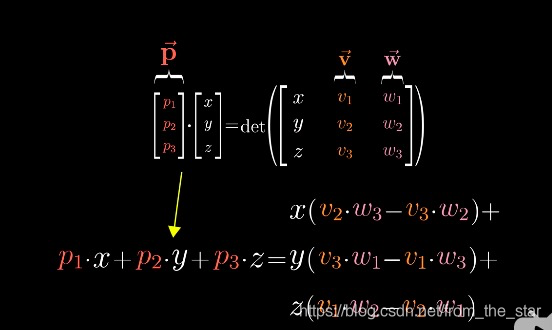前端：推荐一款开源免费的浏览器端Markdown编辑器Vditor

article/2025/11/3 7:02:55

目前程序员的世界到处都是Markdown ，比如CSDN、简书、GitCha、 GitHub、掘金社区等等都支持Markdown文档，另外近几年许多官方技术文档都是使用Markdown来写的。使用Markdown不仅可以非常方便的写博客、写技术文档，而且可以直接导出对应的网站内容，导出可打印的文档，另外Markdown的语法有非常简单，对于程序员来说几乎没有嘘唏成本，且一旦你掌握了它，你就可以在任何地方任何平台使用Markdown来编写技术博客。

今天给大家聊聊一款开源免费的浏览器端Markdown编辑器——Vditor，非常的好用，不仅支持桌面软件、也可以作为前端MarkDown编辑器嵌入到你的系统里面去，现在带大家来了解一下这个非常棒的开源编辑器！

一、编辑器简介

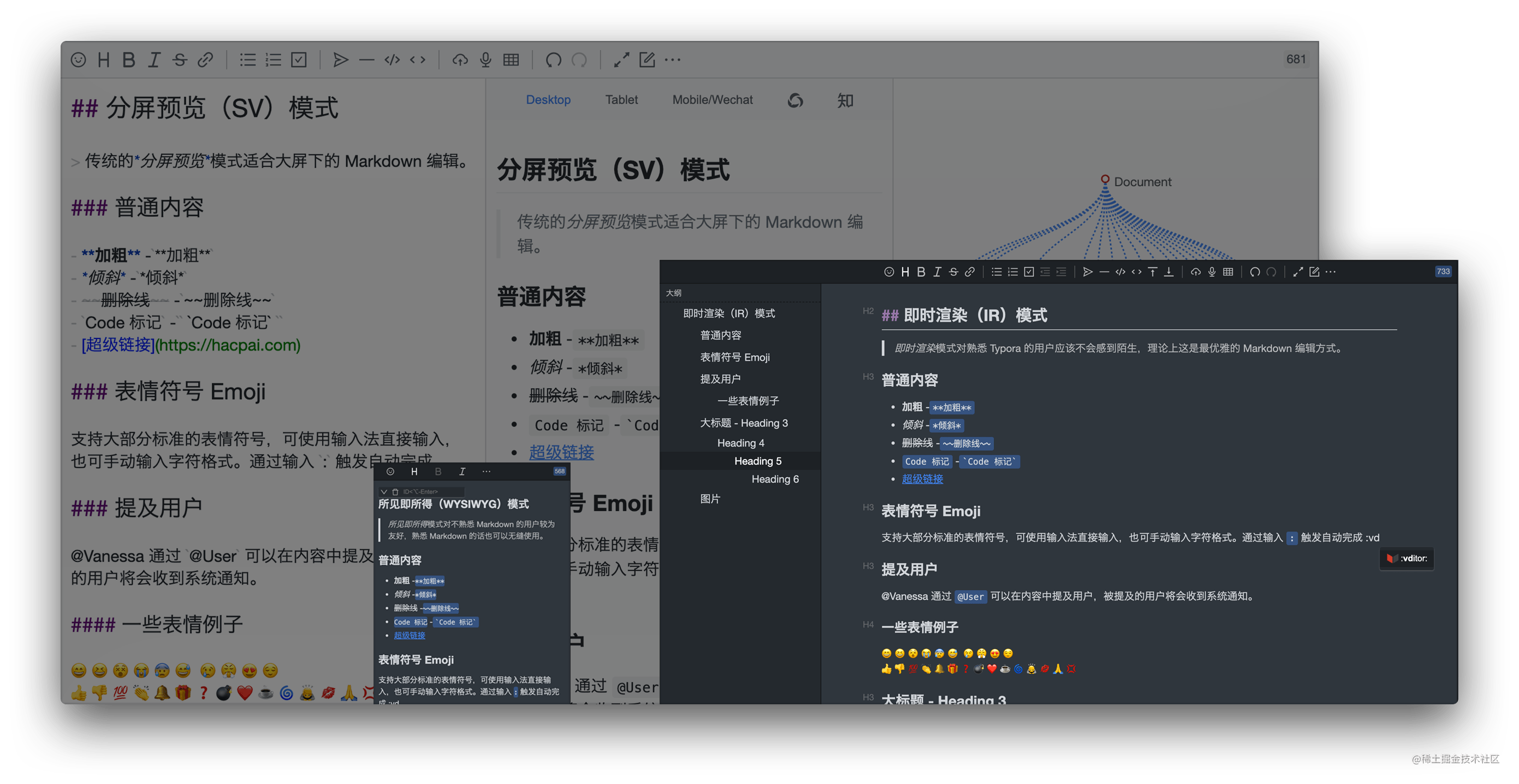
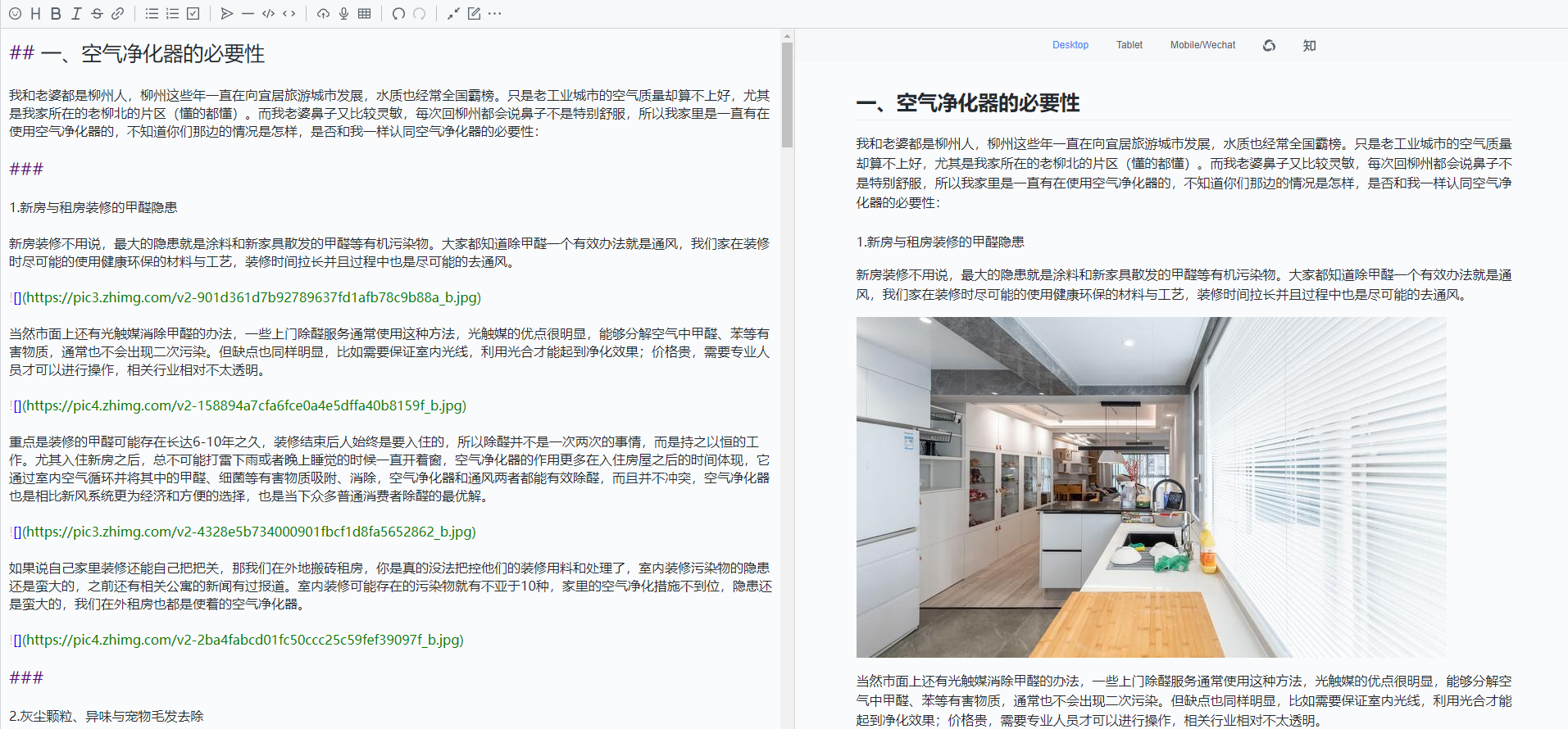
Vditor 是一款浏览器端的 Markdown 编辑器，支持所见即所得、即时渲染（类似 Typora）和分屏预览模式。它使用 TypeScript 实现，支持原生 JavaScript、Vue、React 和 Angular。提供桌面版。支持Windows、Linux、MacOS、浏览器扩展、安卓、IOS版本。

官网：https://b3log.org/vditor/

GitHub：https://github.com/Vanessa219/vditor

桌面版下载：https://b3log.org/siyuan/download.html

二、功能特性

● 支持三种编辑模式：所见即所得（wysiwyg）、即时渲染（ir）、分屏预览（sv）

● 支持大纲、数学公式、脑图、图表、流程图、甘特图、时序图、五线谱、多媒体、语音阅读、标题锚点、代码高亮及复制、graphviz、PlantUML 渲染

● 内置安全过滤、导出、图片懒加载、任务列表、多平台预览、多主题切换、复制到微信公众号/知乎功能

● 实现 CommonMark 和 GFM 规范，可对 Markdown 进行格式化和语法树查看，并支持10+项配置

● 工具栏包含 36+ 项操作，除支持扩展外还可对每一项中的快捷键、提示、提示位置、图标、点击事件、类名、子工具栏进行自定义

● 表情/at/话题等自动补全扩展

● 可使用拖拽、剪切板粘贴上传，显示实时上传进度，支持 CORS 跨域上传

● 实时保存内容，防止意外丢失

● 录音支持，用户可直接发布语音

● 粘贴 HTML 自动转换为 Markdown，如粘贴中包含外链图片可通过指定接口上传到服务器

● 支持主窗口大小拖拽、字符计数

● 多主题支持，内置黑白绿三套主题

● 多语言支持，内置中、英、韩文本地化

● 支持主流浏览器，对移动端友好

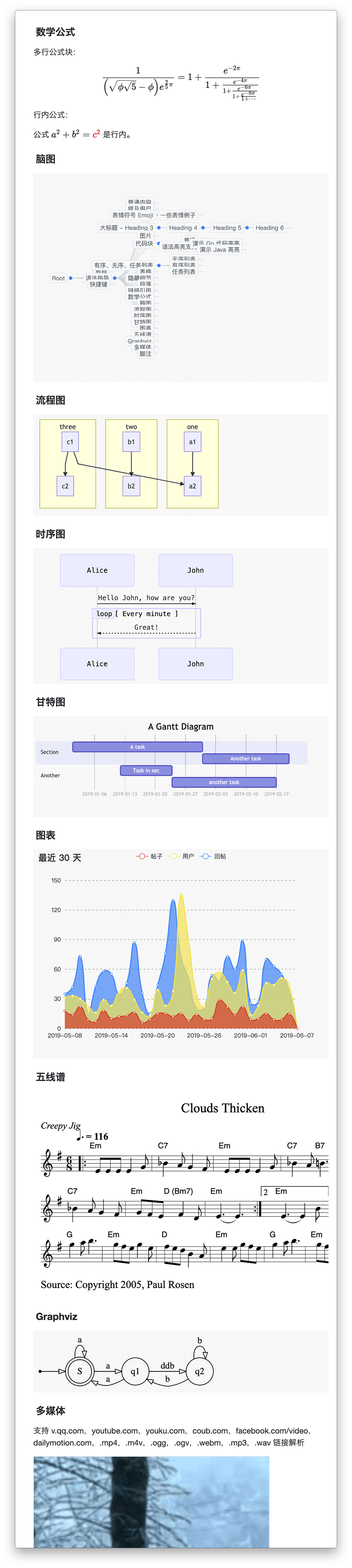
三、编辑器模式初始化设定

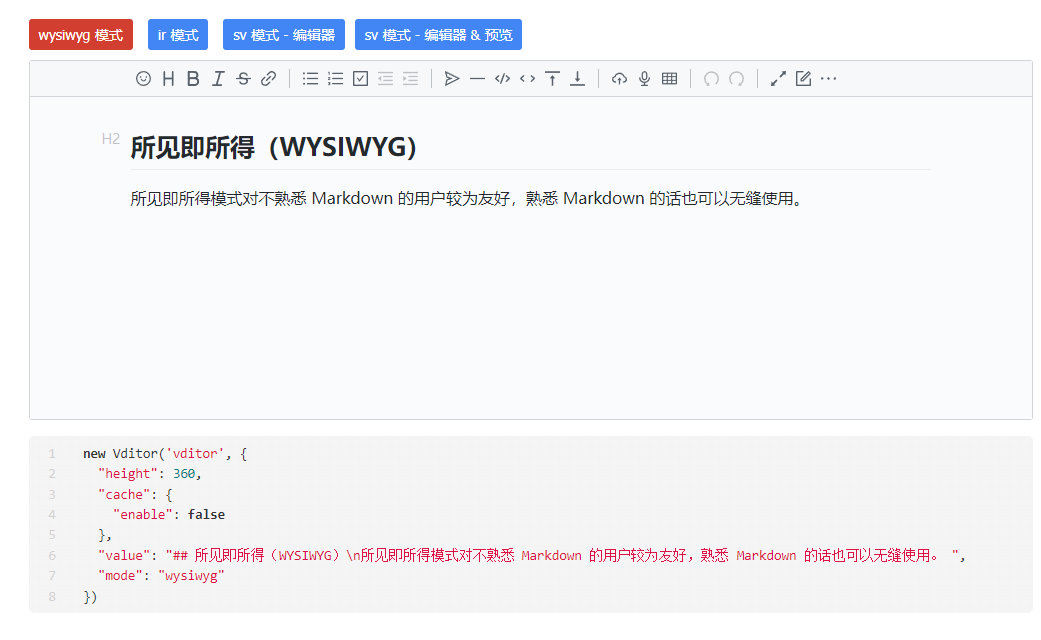
2.1 所见即所得模式

即所得模式对不熟悉 Markdown 的用户较为友好，熟悉 Markdown 的话也可以无缝使用。

new Vditor('vditor', {"height": 360,"cache": {"enable": false},"value": "## 所见即所得（WYSIWYG）\n所见即所得模式对不熟悉 Markdown 的用户较为友好，熟悉 Markdown 的话也可以无缝使用。 ","mode": "wysiwyg"
})

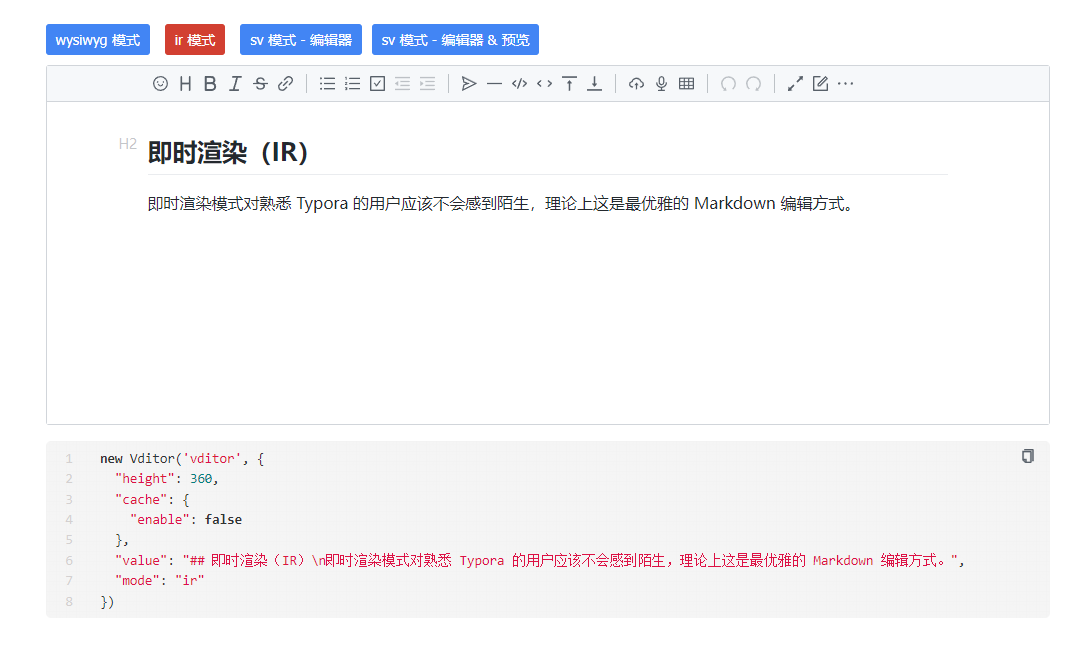
2.2 即时渲染模式

对熟悉 Typora 的用户应该不会感到陌生，理论上这是最优雅的 Markdown 编辑方式。

new Vditor('vditor', {"height": 360,"cache": {"enable": false},"value": "## 即时渲染（IR）\n即时渲染模式对熟悉 Typora 的用户应该不会感到陌生，理论上这是最优雅的 Markdown 编辑方式。","mode": "ir"
})

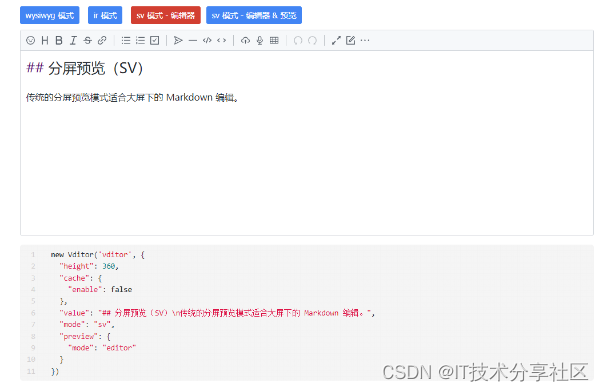
2.3 分屏预览（SV）

该模式目前没有发现具体的使用场景。

new Vditor('vditor', {"height": 360,"cache": {"enable": false},"value": "## 分屏预览（SV）\n传统的分屏预览模式适合大屏下的 Markdown 编辑。","mode": "sv","preview": {"mode": "editor"}
})

在这里插入图片描述

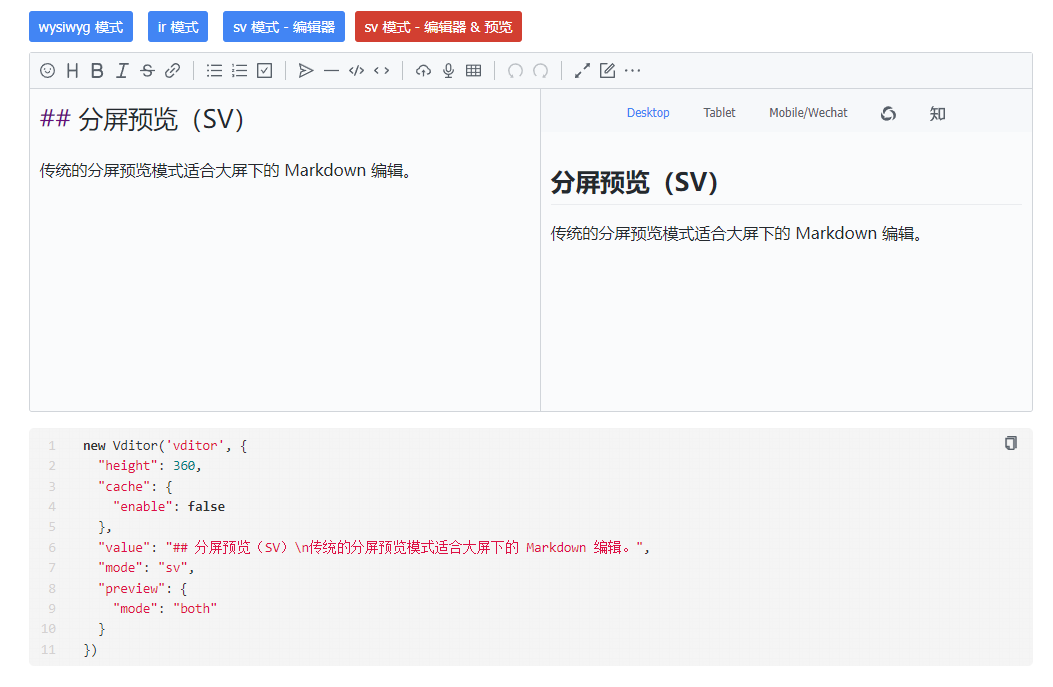
2.4 分屏预览模式

分屏预览（SV）\n传统的分屏预览模式适合大屏下的 Markdown 编辑

new Vditor('vditor', {"height": 360,"cache": {"enable": false},"value": "## 分屏预览（SV）\n传统的分屏预览模式适合大屏下的 Markdown 编辑。","mode": "sv","preview": {"mode": "both"}
})

四、案例代码

直接采用最原始的html提供完整的示例代码，直接可以运行。

<html><head><title>vditor编辑器</title><link rel="stylesheet" href="https://unpkg.com/vditor/dist/index.css" /><script src="https://unpkg.com/vditor/dist/index.min.js"></script></head>    <body><input type="button" onclick="getContent()" value="确定" /><div id="content"></div><script>var vditor = null;window.onload = function() {vditor = new Vditor(document.getElementById('content'), {cache: {enable: false},"mode": "sv","preview": {"mode": "both"}});}// 测试数据填充function getContent() {vditor.setValue("## 测试 \n ### 二级标题 ");}</script></body></html>